案例

GodX...大约 10 分钟

同构字符串(简)

给定两个字符串 s 和 t ，判断它们是否是同构的。

如果 s 中的字符可以按某种映射关系替换得到 t ，那么这两个字符串是同构的。

每个出现的字符都应当映射到另一个字符，同时不改变字符的顺序。不同字符不能映射到同一个字符上，相同字符只能映射到同一个字符上，字符可以映射到自己本身。

示例 1:

输入：s = "egg", t = "add"
输出：true

示例 2：

输入：s = "foo", t = "bar"
输出：false

示例 3：

输入：s = "paper", t = "title"
输出：true

提示：

1 <= s.length <= 5 * 104
t.length == s.length
s 和 t 由任意有效的 ASCII 字符组成

解题思路

我们维护两张哈希表，第一张哈希表s2t以 s 中字符为键，映射至t的字符为值，第二张哈希表 t2s以t中字符为键，映射至s的字符为值。从左至右遍历两个字符串的字符，不断更新两张哈希表，如果出现冲突（即当前下标 index 对应的字符 s[index]已经存在映射且不为t[index] 或当前下标 index 对应的字符t[index]已经存在映射且不为s[index])时说明两个字符串无法构成同构，返回 false。

// 函数名称：isIsomorphic
// 描述：检查两个字符串是否同构，即一个字符串中的字符能够一一对应到另一个字符串中。
// 参数：
//   - s: 第一个字符串
//   - t: 第二个字符串
// 返回值：如果两个字符串同构，则返回 true，否则返回 false。
var isIsomorphic = function (s, t) {
    // 用于存储从 s 到 t 的字符映射关系
    const s2t = {};
    // 用于存储从 t 到 s 的字符映射关系
    const t2s = {};
    // 获取字符串的长度，假设两个字符串的长度相等
    const len = s.length;

    // 遍历字符串的每个字符
    for (let i = 0; i < len; ++i) {
        const x = s[i], y = t[i];

        // 如果 s 中的字符 x 已经有映射且映射的字符不是 y，或者 t 中的字符 y 已经有映射且映射的字符不是 x
        if ((s2t[x] && s2t[x] !== y) || (t2s[y] && t2s[y] !== x)) {
            // 则说明两个字符串不同构，返回 false
            return false;
        }

        // 将当前字符 x 到字符 y 的映射关系存储到 s2t 中
        s2t[x] = y;
        // 将当前字符 y 到字符 x 的映射关系存储到 t2s 中
        t2s[y] = x;
    }

    // 如果遍历完所有字符都没有发现不同构的情况，则说明两个字符串是同构的，返回 true
    return true;
};

两数之和(简)

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

解题思路

双层for循环暴力破解
map 哈希表优化，避免多余的循环

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */

// 暴力破解
var twoSum = function(nums, target) {
    for(let i = 0;i < nums.length - 1;i++) {
         for(let j = i + 1; j < nums.length; j++) {
             if(nums[i] + nums[j] === target) {
                 return [i,j]
            }
         }
     }
};

// hash表
var twoSum = function(nums, target) {
    let map = new Map();
    for(let i = 0; i < nums.length;i++) {
        let other = target - nums[i]
        if(map.has(other)) {
            return [i,map.get(other)]
        } else {
            map.set(nums[i],i)
        }
    }
};

存在重复元素 II(简)

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [1,2,3,1], k = 3
输出：true

示例 2：

输入：nums = [1,0,1,1], k = 1
输出：true

示例 3：

输入：nums = [1,2,3,1,2,3], k = 2
输出：false

提示：

1 <= nums.length <= 105
-109 <= nums[i] <= 109
0 <= k <= 105

解题思路

利用 hash 表记录，以此来判断是否存在重复元素

var containsNearbyDuplicate = function (nums, k) {
    const map = new Map();
    const length = nums.length;
    for (let i = 0; i < length; i++) {
        const num = nums[i];
        if (map.has(num) && i - map.get(num) <= k) {
            return true;
        }
        map.set(num, i);
    }
    return false;
};

快乐数(中)

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

提示：

1 <= n <= 231 - 1

解题思路

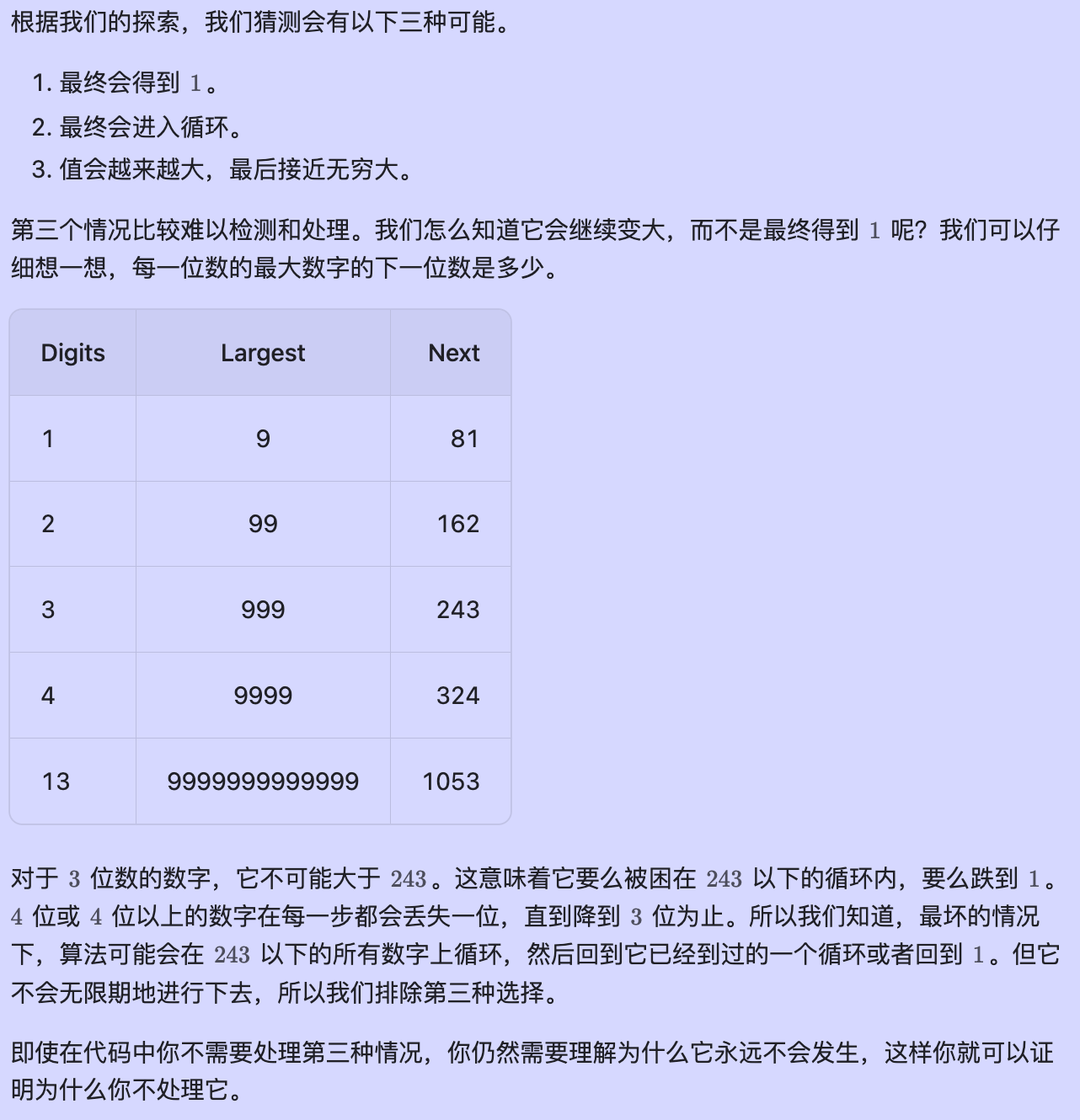
具体流程：

定义一个辅助函数get_next，用来计算一个数的每个数字的平方和。
定义一个集合seen，用来存储已经出现过的数，避免无限循环。
用一个while循环，不断更新n的值，直到n等于1或者已经在seen中。
如果n等于1，返回true，表示这个数是快乐数；否则返回false，表示这个数不是快乐数。

// 函数判断一个数字是否是快乐数
function isHappy(n) {
    // 内部辅助函数，计算下一个数字
    function get_next(number) {
        let total_sum = 0;
        // 循环，计算每个数字的平方并相加
        while (number > 0) {
            // 取出数字的个位
            let digit = number % 10;
            // 去掉数字的个位，保留其余部分
            number = Math.floor(number / 10);
            // 将个位数字的平方加到总和中
            total_sum += digit ** 2;
        }
        return total_sum;
    }

    // 用于存储已经出现过的数字的集合
    let seen = new Set();

    // 当输入数字不为1且未出现在集合中时，继续循环
    while (n !== 1 && !seen.has(n)) {
        // 将当前数字加入集合
        seen.add(n);
        // 获取下一个数字
        n = get_next(n);
    }

    // 最终判断是否为快乐数，返回布尔值
    return n === 1;
}

字母异位词分组(中)

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

示例 2:

输入: strs = [""]
输出: [[""]]

示例 3:

输入: strs = ["a"]
输出: [["a"]]

提示：

1 <= strs.length <= 104
0 <= strs[i].length <= 100
strs[i] 仅包含小写字母

解题思路

使用一个Map对象来存储变位词分组的结果，键为字符串排序后的形式，值为一个包含变位词的数组。
遍历字符串数组，对每个字符串进行以下操作：
- 将字符串排序后作为键，如果键已经存在于Map对象中，就将字符串添加到对应的值数组中；如果键不存在，就创建一个新的键值对，值为一个只包含字符串的数组。
返回Map对象的值数组，即变位词分组的结果。

/**
 * @param {string[]} strs
 * @return {string[][]}
 */
var groupAnagrams = function(strs) {
    const map = new Map();
    for (let str of strs) {
        // 将字符串排序后作为键
        const key = [...str].sort().join('');
        // 如果键已经存在，将字符串添加到对应的值数组中
        if (map.has(key)) {
            map.get(key).push(str);
        // 如果键不存在，创建一个新的键值对，值为一个只包含字符串的数组
        } else {
            map.set(key, [str]);
        }
    }
    // 返回值数组，即变位词分组的结果
    return [...map.values()];
};

最长连续序列(中)

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

提示：

0 <= nums.length <= 105
-109 <= nums[i] <= 109

解题思路

先排序数组，然后遍历并统计连续序列的长度，最后返回最长连续序列的长度。

self

/**
 * @param {number[]} nums
 * @return {number}
 */
var longestConsecutive = function (nums) {
    const arr = []
    if (nums.length === 0) return 0;
    const len = nums.length;
    nums.sort((a, b) => a - b);
    console.log(nums)
    let ans = 1;
    for (let i = 0; i < nums.length; i++) {
        console.log(i, nums[i + 1] - nums[i])
        if (nums[i + 1] - nums[i] === 1) {
            ans++
        } else if (nums[i + 1] === nums[i]) {
            continue;
        } else if (nums[i + 1] - nums[i] > 1 && ans < len - i + 1) {
            arr.push(ans)
            ans = 1;
            continue;
        } else {
            arr.push(ans)
            return Math.max(...arr);
        }
    }
};

优化后

var longestConsecutive = function(nums) {
    if (nums.length === 0) {
        return 0;
    }
    // 去重
    const uniqueNums = Array.from(new Set(nums));
    // 排序
    uniqueNums.sort((a, b) => a - b);
    let currentStreak = 1;
    let longestStreak = 1;
    for (let i = 1; i < uniqueNums.length; i++) {
        if (uniqueNums[i] === uniqueNums[i - 1] + 1) {
            // 发现连续序列
            currentStreak++;
        } else if (uniqueNums[i] !== uniqueNums[i - 1]) {
            // 重置连续序列计数
            currentStreak = 1;
        }
        // 更新最长连续序列长度
        longestStreak = Math.max(longestStreak, currentStreak);
    }
    return longestStreak;
};

优质数对的总数 II(中)

给你两个整数数组 nums1 和 nums2，长度分别为 n 和 m。同时给你一个正整数 k。

如果 nums1[i] 可以被 nums2[j] * k 整除，则称数对 (i, j) 为 优质数对（0 <= i <= n - 1, 0 <= j <= m - 1）。

返回 优质数对 的总数。

示例 1：

**输入：**nums1 = [1,3,4], nums2 = [1,3,4], k = 1

**输出：**5

解释：

5个优质数对分别是 (0, 0), (1, 0), (1, 1), (2, 0), 和 (2, 2)。

示例 2：

**输入：**nums1 = [1,2,4,12], nums2 = [2,4], k = 3

**输出：**2

解释：

2个优质数对分别是 (3, 0) 和 (3, 1)。

提示：

1 <= n, m <= 105
1 <= nums1[i], nums2[j] <= 106
1 <= k <= 103

解题思路

初始化计数器：
- cnt1是一个计数器，它计算nums1中所有能被k整除的元素除以k后的结果的数量。这通过列表推导式和Counter类实现。
检查计数器是否为空：
- 如果cnt1为空，即没有任何元素能被k整除，则直接返回0。
初始化答案变量：
- ans用于存储最终的答案。
找到最大的cnt1键值：
- u被设置为cnt1中的最大键值，这代表nums1中元素除以k后可能的最大结果。
遍历nums2并更新答案：
- 对于nums2中的每个元素x及其计数cnt，代码计算所有x的倍数y（其中y是cnt1的键），并将这些y对应的计数相加，得到s。
- 然后，将s乘以x在nums2中出现的次数cnt，并加到ans上。
返回最终答案：
- 函数返回ans，即满足条件的元素对的数量。

这个算法的核心思想是利用计数器来快速统计和查询特定条件下的元素数量，从而避免了对每个元素对的直接比较，提高了效率。

from collections import Counter
from typing import List


class Solution:
    def numberOfPairs(self, nums1: List[int], nums2: List[int], k: int) -> int:
        # 创建一个计数器 cnt1，用于统计 nums1 中能被 k 整除的元素除以 k 后的结果的数量
        cnt1 = Counter(x // k for x in nums1 if x % k == 0)

        # 如果 cnt1 为空，即没有任何元素能被 k 整除，则直接返回 0
        if not cnt1:
            return 0

        # 初始化答案变量 ans
        ans = 0

        # 找到 cnt1 中的最大键值 u，代表 nums1 中元素除以 k 后可能的最大结果
        u = max(cnt1)

        # 遍历 nums2 中的每个元素 x 及其计数 cnt
        for x, cnt in Counter(nums2).items():
            # 计算所有 x 的倍数 y（其中 y 是 cnt1 的键）的计数之和 s
            s = sum(cnt1[y] for y in range(x, u + 1, x))  # 枚举 x 的倍数

            # 将 s 乘以 x 在 nums2 中出现的次数 cnt，并加到 ans 上
            ans += s * cnt

        # 返回最终答案 ans
        return ans

昵称

邮箱

网址

按正序
按倒序
按热度

案例

同构字符串(简)

两数之和(简)

存在重复元素 II(简)

快乐数(中)

字母异位词分组(中)

最长连续序列(中)

优质数对的总数 II(中)

预览: