案例

岛屿数量（中）

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] 的值为 '0' 或 '1'

解题思路

• 使用双重循环遍历整个网格。
• 当找到一个未访问的陆地时，增加岛屿数量，并从该位置开始进行深度优先搜索（DFS）。
• DFS函数将所有相连的陆地标记为已访问。
• inArea函数用于检查给定的位置是否在网格的范围内。

这样，每个岛屿都会被正确地计数，而不会重复或遗漏。

var numIslands = function (grid) {
    let res = 0; // 初始化岛屿数量为0

    // 遍历网格的每一行
    for (let i = 0; i < grid.length; i++) {
        // 遍历网格的每一列
        for (let j = 0; j < grid[0].length; j++) {
            // 如果当前位置是陆地（用'1'表示）
            if (grid[i][j] === '1') {
                res++; // 岛屿数量加1
                dfs(grid, i, j); // 从当前位置开始深度优先搜索，标记所有相连的陆地
            }
        }
    }
    return res; // 返回岛屿数量
};

// 深度优先搜索函数，用于标记所有相连的陆地
function dfs(grid, r, c) {
    // 如果当前位置超出网格范围，返回
    if (!inArea(grid, r, c)) return;
    // 如果当前位置不是陆地，返回
    if (grid[r][c] !== '1') return;

    // 将当前位置标记为已访问（用'2'表示）
    grid[r][c] = '2';

    // 递归搜索上、下、左、右四个方向
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

// 函数用于检查给定位置是否在网格范围内
function inArea(grid, r, c) {
    return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}

被围绕的区域（中）

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获 所有 被围绕的区域：

• **连接：**一个单元格与水平或垂直方向上相邻的单元格连接。
• 区域：连接所有 '0' 的单元格来形成一个区域。
• **围绕：**如果您可以用 'X' 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

通过将输入矩阵 board 中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。

示例 1：

**输入：**board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]

输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]

解释：

img

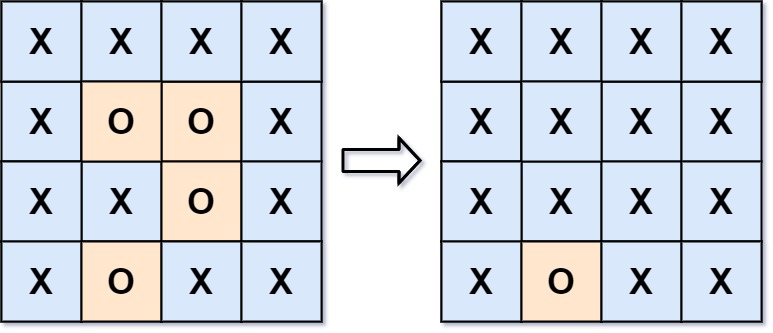
在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

**输入：**board = [["X"]]

输出：[["X"]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 'X' 或 'O'

解题思路

1. 遍历棋盘的四条边缘，对每个边缘上的 ‘O’ 进行 DFS。
2. 在 DFS 过程中，将所有与边缘相连的 ‘O’ 标记为一个特殊字符（例如 ‘2’），表示这些 ‘O’ 不应该被替换。
3. 遍历整个棋盘，将所有未被标记的 ‘O’ 替换为 ‘X’。
4. 再次遍历棋盘，将所有标记为特殊字符的 ‘O’ 恢复为 ‘O’。

通过这种方式，我们确保了只有被围绕的 ‘O’ 被替换，而边缘上的 ‘O’ 保持不变。这样做的好处是，我们只需要遍历一次棋盘的边缘，然后在最后再遍历一次整个棋盘，就可以完成所有的替换操作。

var solve = function(board) {
    const m = board.length;
    if (m === 0) return; // 如果棋盘为空，直接返回

    const n = board[0].length;

    // 从边缘开始进行 DFS，标记所有与边缘相连的 'O' 为 '2'
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            // 检查边缘的 'O'
            if (i === 0 || i === m - 1 || j === 0 || j === n - 1) {
                if (board[i][j] === 'O') {
                    dfs(board, i, j);
                }
            }
        }
    }

    // 遍历整个 board，将 'O' 转换为 'X'，将 '2' 转换回 'O'
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (board[i][j] === 'O') {
                board[i][j] = 'X'; // 被围绕的 'O' 转换为 'X'
            } else if (board[i][j] === '2') {
                board[i][j] = 'O'; // 恢复与边缘相连的 'O'
            }
        }
    }
};

function dfs(board, i, j) {
    if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) return;
    if (board[i][j] !== 'O') return;

    board[i][j] = '2'; // 将边缘的 'O' 和与之相连的 'O' 标记为 '2'

    // 递归地标记所有相连的 'O'
    dfs(board, i - 1, j);
    dfs(board, i + 1, j);
    dfs(board, i, j - 1);
    dfs(board, i, j + 1);
}

克隆图（中）

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例 1：

img

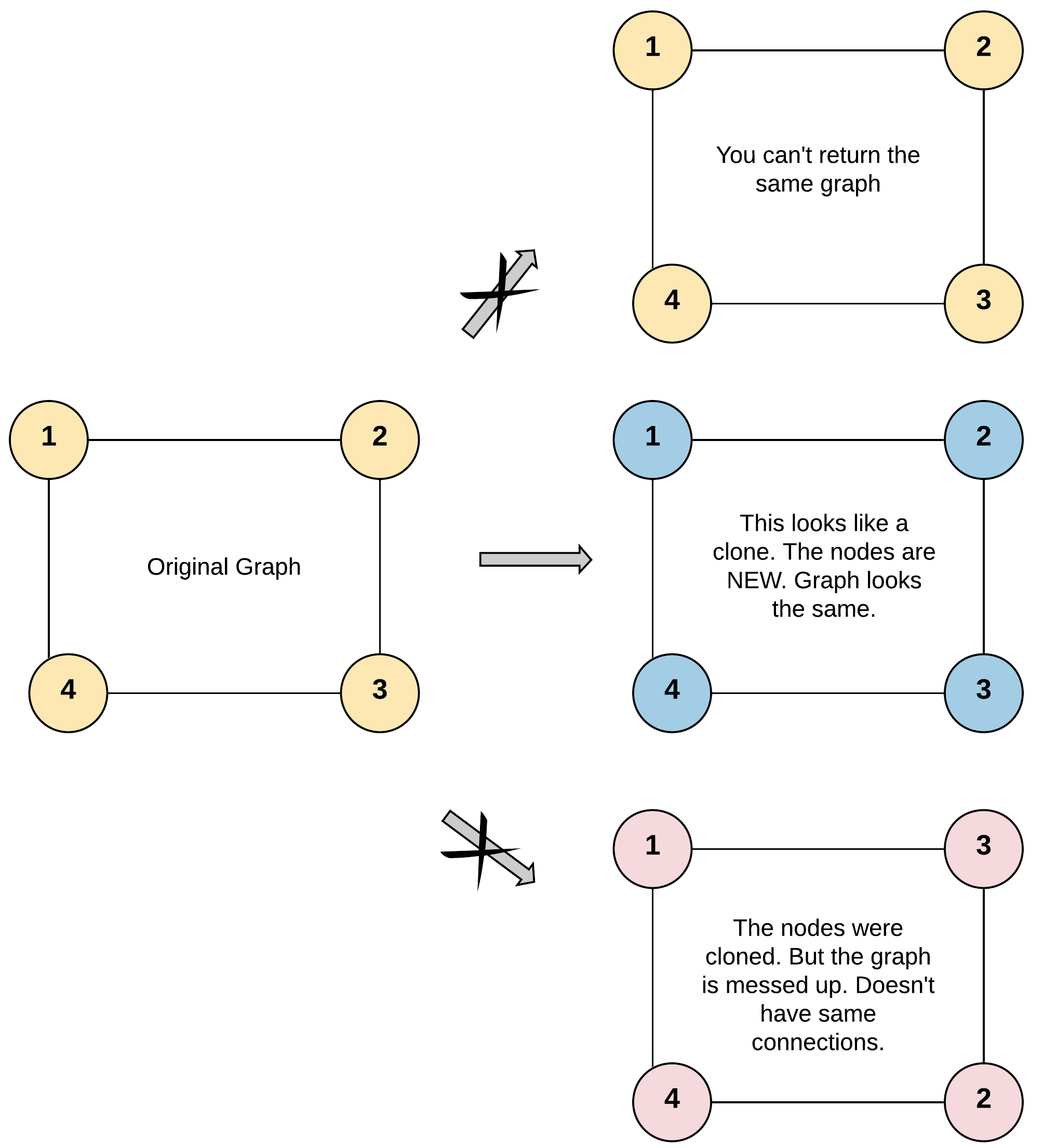
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

img

输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

提示：

• 这张图中的节点数在 [0, 100] 之间。
• 1 <= Node.val <= 100
• 每个节点值 Node.val 都是唯一的，
• 图中没有重复的边，也没有自环。
• 图是连通图，你可以从给定节点访问到所有节点。

解题思路

DFS

1. 输入检查：首先检查输入节点是否为空。如果是，则直接返回，因为没有图可以克隆。
2. 初始化：创建一个映射 visited，用于存储原始节点和它们的克隆节点之间的对应关系。
3. 深度优先搜索（DFS）：定义一个递归函数 dfs，用于遍历图并克隆节点。
   • 对于每个节点 n，创建一个新节点 nCopy，其值与 n 相同。
   • 在 visited 映射中记录 n 和 nCopy 的关系。
   • 遍历 n的所有邻居ne。
     • 如果 ne 还没有被访问过（即不在 visited 中），则递归地对 ne 执行 dfs。
     • 将 ne 的克隆节点（已在 visited 中）添加到 nCopy 的邻居列表中。
4. 克隆图：从输入节点开始执行 dfs，以克隆整个图。
5. 返回结果：返回输入节点的克隆节点，作为克隆图的起始节点。

通过这种方式，函数能够递归地遍历整个图，并创建每个节点的副本，同时保持节点间的邻居关系不变。最终，它返回一个与原始图结构相同的新图。

BFS

广度优先搜索是一种遍历或搜索树或图的算法，它从根节点开始，一层层地向外扩展。以下是这个算法的主要步骤：

1. 输入检查：首先检查输入节点是否为空。如果是，则直接返回，因为没有图可以克隆。
2. 初始化：创建一个映射 visited，用于存储原始节点和它们的克隆节点之间的对应关系。同时，将输入节点和其克隆节点存入 visited，并加入一个队列 q。
3. 广度优先搜索（BFS）：使用一个队列 q 来实现广度优先搜索。
   • 当队列不为空时，循环执行以下步骤：
     • 从队列中取出一个节点 n。
     • 遍历 n 的所有邻居 ne。
       • 如果 ne 还没有被访问过（即不在 visited 中），则将其加入队列 q，并在 visited 中为其创建一个克隆节点。
       • 将 ne 的克隆节点（已在 visited 中）添加到 n 的克隆节点的邻居列表中。
4. 返回结果：当所有节点都被访问并克隆后，返回输入节点的克隆节点，作为克隆图的起始节点。

通过这种方式，函数能够逐层遍历整个图，并创建每个节点的副本，同时保持节点间的邻居关系不变。最终，它返回一个与原始图结构相同的新图。广度优先搜索特别适合于这种类型的图遍历，因为它可以确保在访问更远的节点之前，所有相邻的节点都已被访问和处理。

DFS

var cloneGraph = function (node) {
    // 如果节点为空，则直接返回
    if (!node) return;

    // 创建一个映射来存储原始节点和克隆节点之间的映射关系
    const visited = new Map();

    // 定义一个深度优先搜索（DFS）函数来克隆节点及其邻居
    const dfs = (n) => {
        // 创建一个新节点，其值与原始节点相同
        const nCopy = new Node(n.val);
        // 在映射中记录原始节点和克隆节点的关系
        visited.set(n, nCopy);

        // 遍历原始节点的所有邻居
        (n.neighbors || []).forEach(ne => {
            // 如果邻居节点还没有被访问过（即还没有被克隆），则递归克隆它
            if (!visited.has(ne)) {
                dfs(ne);
            }
            // 将克隆的邻居节点添加到克隆节点的邻居列表中
            nCopy.neighbors.push(visited.get(ne));
        })
    }

    // 从给定节点开始深度优先搜索，克隆整个图
    dfs(node);

    // 返回克隆的起始节点
    return (visited.get(node));
};

BFS

var cloneGraph = function(node) {
    if(!node) return;
    const visited = new Map();
    visited.set(node, new Node(node.val));//节点值和新建节点以键值对存入visited
    const q = [node];
    while(q.length) {
        const n = q.shift()//出队
        (n.neighbors || []).forEach(ne => {//循环相邻节点
            if(!visited.has(ne)) {//没有访问过就加入队列
                q.push(ne);
                visited.set(ne, new Node(ne.val));
            }
            visited.get(n).neighbors.push(visited.get(ne));//复制相邻节点
        })
    }
    return visited.get(node);
};

除法求值（中）

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

**注意：**输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

**注意：**未在等式列表中出现的变量是未定义的，因此无法确定它们的答案。

示例 1：

输入：equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意：x 是未定义的 => -1.0

示例 2：

输入：equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出：[3.75000,0.40000,5.00000,0.20000]

示例 3：

输入：equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出：[0.50000,2.00000,-1.00000,-1.00000]

提示：

• 1 <= equations.length <= 20
• equations[i].length == 2
• 1 <= Ai.length, Bi.length <= 5
• values.length == equations.length
• 0.0 < values[i] <= 20.0
• 1 <= queries.length <= 20
• queries[i].length == 2
• 1 <= Cj.length, Dj.length <= 5
• Ai, Bi, Cj, Dj 由小写英文字母与数字组成

图

// 定义两个全局变量，grah 用于存储图的结构，visited 用于存储已访问的节点
let grah;
let visited;

// 主函数 calcEquation，接收方程组、值和查询
var calcEquation = function (equations, values, queries) {
    // 初始化 grah 和 visited
    grah = Object.create(null); // 创建一个空的 grah 对象
    visited = new Set(); // 创建一个空的 Set 对象用于存储已访问的节点

    // 遍历 values 数组，构建图结构
    for (let i = 0; i < values.length; i++) {
        const x = equations[i][0], y = equations[i][1], value = values[i];
        // 如果 x 不在 grah 中，添加 x 作为键
        if (!grah[x]) grah[x] = Object.create(null);
        // 设置 x 到 y 的值为 value
        grah[x][y] = value;
        // 如果 y 不在 grah 中，添加 y 作为键
        if (!grah[y]) grah[y] = Object.create(null);
        // 设置 y 到 x 的值为 1 / value
        grah[y][x] = 1 / value;
    }

    // 遍历查询数组 queries，并使用 d 函数处理每个查询
    return queries.map(([x, y]) => d(x, y));
};

// 辅助函数 d，用于在图中查找从 x 到 y 的路径
const d = (x, y) => {
    // 如果 x 不在 grah 中，返回 -1
    if (!grah[x]) return -1;
    // 如果 x 到 y 的路径已知，返回该值
    if (grah[x][y]) return grah[x][y];

    // 获取 x 的所有邻居
    let k = Object.keys(grah[x]), i = -1;
    // 遍历 x 的邻居
    while (++i < k.length) {
        // 如果邻居未被访问过
        if (!visited.has(k[i])) {
            visited.add(k[i]); // 标记为已访问
            const t = d(k[i], y); // 递归查找从邻居到 y 的路径
            visited.delete(k[i]); // 恢复未访问状态
            // 如果找到了路径，返回路径值的乘积
            if (t !== -1) return grah[x][k[i]] * t;
        }
    }
    // 如果没有找到路径，返回 -1
    return -1;
}

二维数组 + 哈希表

var calcEquation = function(equations, values, queries) {
    grah = []
    let i = -1, id = 0, h = new Map
    while (++i < values.length) {
        const x = equations[i][0], y = equations[i][1], value = values[i]
        if (!h.has(x)) h.set(x, id++)
        if (!h.has(y)) h.set(y, id++)
        const idX = h.get(x), idY = h.get(y)
        if (!grah[idX]) grah[idX] = []
        grah[idX][idY] = value
        if (!grah[idY]) grah[idY] = []
        grah[idY][idX] = 1 / value
    }
    visited = new Uint8Array(id)
    return queries.map(([x, y]) => d(h.get(x), h.get(y)))
};
let grah, visited, d = (x, y) => {
    if (!grah[x]) return -1
    if (grah[x][y]) return grah[x][y]
    for (let i = 0; i < grah[x].length; i++) 
        if (grah[x][i] !== void 0 && visited[i] === 0) {
            visited[i] = 1
            const t = d(i, y)
            visited[i] = 0
            if(t !== -1) return grah[x][i] * t
        }
    return -1;
}

并查集

class UnionFind {
    constructor (n) {
        this.parent = new Uint8Array(n)
        this.weight = new Float32Array(n)
        while (n--) {
            this.parent[n] = n
            this.weight[n] = 1.0
        }
    }
    union (x, y, value) {
        const rootX = this.find(x), rootY = this.find(y)
        if (rootX !== rootY) {
            this.parent[rootX] = rootY
            this.weight[rootX] = this.weight[y] * value / this.weight[x]
        }
    }
    find (x) {
        if (x !== this.parent[x]) {
            const orginX = this.parent[x]
            this.parent[x] = this.find(this.parent[x])
            this.weight[x] *= this.weight[orginX]
        } 
        return this.parent[x]
    }
    isConnected (x, y) {
        const rootX = this.find(x), rootY = this.find(y)
        return rootX !== void 0 && rootX === rootY ? this.weight[x] / this.weight[y] : -1.0
    }
}

var calcEquation = function(equations, values, queries) {
    const unionFind = new UnionFind(values.length << 1), h = new Map
    for (let i = 0, id = 0; i < values.length; i++) {
        const x = equations[i][0], y = equations[i][1]
        if (!Array.from(h.keys()).includes(x)) h.set(x, id++)
        if (!Array.from(h.keys()).includes(y)) h.set(y, id++)
        unionFind.union(h.get(x), h.get(y), values[i])
    }
    return queries.map(([x, y]) => unionFind.isConnected(h.get(x), h.get(y)))
};

Floyd 算法

var calcEquation = function(equations, values, queries) {
    let nvars = 0;
    const variables = new Map();

    const n = equations.length;
    for (let i = 0; i < n; i++) {
        if (!variables.has(equations[i][0])) {
            variables.set(equations[i][0], nvars++);
        }
        if (!variables.has(equations[i][1])) {
            variables.set(equations[i][1], nvars++);
        }
    }
    const graph = new Array(nvars).fill(0).map(() => new Array(nvars).fill(-1.0));
    for (let i = 0; i < n; i++) {
        const va = variables.get(equations[i][0]), vb = variables.get(equations[i][1]);
        graph[va][vb] = values[i];
        graph[vb][va] = 1.0 / values[i];
    }

    for (let k = 0; k < nvars; k++) {
        for (let i = 0; i < nvars; i++) {
            for (let j = 0; j < nvars; j++) {
                if (graph[i][k] > 0 && graph[k][j] > 0) {
                    graph[i][j] = graph[i][k] * graph[k][j];
                }
            }
        }
    }

    const queriesCount = queries.length;
    const ret = new Array(queriesCount).fill(0);
    for (let i = 0; i < queriesCount; i++) {
        const query = queries[i];
        let result = -1.0;
        if (variables.has(query[0]) && variables.has(query[1])) {
            const ia = variables.get(query[0]), ib = variables.get(query[1]);
            if (graph[ia][ib] > 0) {
                result = graph[ia][ib];
            }
        }
        ret[i] = result;
    }
    return ret;
};

课程表（中）

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

• 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

• 1 <= numCourses <= 2000
• 0 <= prerequisites.length <= 5000
• prerequisites[i].length == 2
• 0 <= ai, bi < numCourses
• prerequisites[i] 中的所有课程对 互不相同

解题思路

题意解释

• 一共有 n 门课要上，编号为 0 ~ n-1。
• 先决条件 [1, 0]，意思是必须先上课 0，才能上课 1。
• 给你 n、和一个先决条件表，请你判断能否完成所有课程。

再举个生活的例子

• 先穿内裤再穿裤子，先穿打底再穿外套，先穿衣服再戴帽子，是约定俗成的。
• 内裤外穿、光着身子戴帽子等，都会有点奇怪。
• 我们遵循穿衣的一条条先后规则，用一串 顺序行为，把衣服一件件穿上。
• 我们遵循课程之间的先后规则，找到一种上课顺序，把所有课一节节上完。

用有向图描述依赖关系

• 示例：n = 6，先决条件表：[[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]]
• 课 0, 1, 2 没有先修课，可以直接选。其余的课，都有两门先修课。
• 我们用有向图来展现这种依赖关系（做事情的先后关系）：

image-20240703110409349

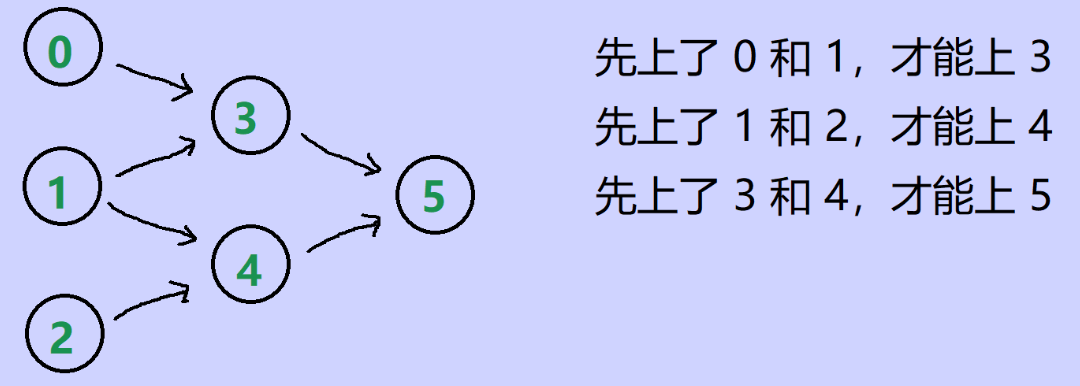
• 这种叫 有向无环图，把一个 有向无环图 转成 线性的排序 就叫 拓扑排序。
• 有向图有 入度 和 出度 的概念：
  • 如果存在一条有向边 A --> B，则这条边给 A 增加了 1 个出度，给 B 增加了 1 个入度。
• 所以，顶点 0、1、2 的入度为 0。顶点 3、4、5 的入度为 2。

每次只能选你能上的课

• 每次只能选入度为 0 的课，因为它不依赖别的课，是当下你能上的课。
• 假设选了 0，课 3 的先修课少了一门，入度由 2 变 1。
• 接着选 1，导致课 3 的入度变 0，课 4 的入度由 2 变 1。
• 接着选 2，导致课 4 的入度变 0。
• 现在，课 3 和课 4 的入度为 0。继续选入度为 0 的课……直到选不到入度为 0 的课。

这很像 BFS

• 让入度为 0 的课入列，它们是能直接选的课。
• 然后逐个出列，出列代表着课被选，需要减小相关课的入度。
• 如果相关课的入度新变为 0，安排它入列、再出列……直到没有入度为 0 的课可入列。

BFS 前的准备工作

• 每门课的入度需要被记录，我们关心入度值的变化。
• 课程之间的依赖关系也要被记录，我们关心选当前课会减小哪些课的入度。
• 因此我们需要选择合适的数据结构，去存这些数据：
• 入度数组：课号 0 到 n - 1 作为索引，通过遍历先决条件表求出对应的初始入度。
• 邻接表：用哈希表记录依赖关系（也可以用二维矩阵，但有点大）
  • key：课号
  • value：依赖这门课的后续课（数组）

怎么判断能否修完所有课？

• BFS 结束时，如果仍有课的入度不为 0，无法被选，完成不了所有课。否则，能找到一种顺序把所有课上完。
• 或者：用一个变量 count 记录入列的顶点个数，最后判断 count 是否等于总课程数。

function canFinish(numCourses, prerequisites) {
    // 创建一个映射，用于存储每个节点的入度和邻接列表
    let graph = new Map();
    for (let i = 0; i < numCourses; i++) {
        graph.set(i, { inDegree: 0, adjacent: [] });
    }

    // 填充邻接列表和入度
    for (let edge of prerequisites) {
        let [to, from] = edge;
        graph.get(to).inDegree++;
        graph.get(from).adjacent.push(to);
    }

    // 找到所有入度为0的节点
    let queue = [];
    for (let [vertex, { inDegree }] of graph) {
        if (inDegree === 0) {
            queue.push(vertex);
        }
    }

    // 进行拓扑排序
    let count = 0;
    while (queue.length > 0) {
        let vertex = queue.shift();
        count++;
        for (let neighbor of graph.get(vertex).adjacent) {
            graph.get(neighbor).inDegree--;
            if (graph.get(neighbor).inDegree === 0) {
                queue.push(neighbor);
            }
        }
    }

    // 判断是否可以完成所有课程
    return count === numCourses;
}

蛇梯棋(中)

给你一个大小为 n x n 的整数矩阵 board ，方格按从 1 到 n2 编号，编号遵循 转行交替方式 ，从左下角开始 （即，从 board[n - 1][0] 开始）每一行交替方向。

玩家从棋盘上的方格 1 （总是在最后一行、第一列）开始出发。

每一回合，玩家需要从当前方格 curr 开始出发，按下述要求前进：

• 选定目标方格 next，目标方格的编号符合范围 [curr + 1, min(curr + 6, n2)] 。
  • 该选择模拟了掷 六面体骰子 的情景，无论棋盘大小如何，玩家最多只能有 6 个目的地。
• 传送玩家：如果目标方格 next 处存在蛇或梯子，那么玩家会传送到蛇或梯子的目的地。否则，玩家传送到目标方格 next 。
• 当玩家到达编号 n2 的方格时，游戏结束。

r 行 c 列的棋盘，按前述方法编号，棋盘格中可能存在 “蛇” 或 “梯子”；如果 board[r][c] != -1，那个蛇或梯子的目的地将会是 board[r][c]。编号为 1 和 n2 的方格上没有蛇或梯子。

注意，玩家在每回合的前进过程中最多只能爬过蛇或梯子一次：就算目的地是另一条蛇或梯子的起点，玩家也 不能 继续移动。

• 举个例子，假设棋盘是 [[-1,4],[-1,3]] ，第一次移动，玩家的目标方格是 2 。那么这个玩家将会顺着梯子到达方格 3 ，但 不能 顺着方格 3 上的梯子前往方格 4 。

返回达到编号为 n2 的方格所需的最少移动次数，如果不可能，则返回 -1。

示例 1：

img

输入：board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
输出：4
解释：
首先，从方格 1 [第 5 行，第 0 列] 开始。 
先决定移动到方格 2 ，并必须爬过梯子移动到到方格 15 。
然后决定移动到方格 17 [第 3 行，第 4 列]，必须爬过蛇到方格 13 。
接着决定移动到方格 14 ，且必须通过梯子移动到方格 35 。 
最后决定移动到方格 36 , 游戏结束。 
可以证明需要至少 4 次移动才能到达最后一个方格，所以答案是 4 。 

示例 2：

输入：board = [[-1,-1],[-1,3]]
输出：1

提示：

• n == board.length == board[i].length
• 2 <= n <= 20
• grid[i][j] 的值是 -1 或在范围 [1, n2] 内
• 编号为 1 和 n2 的方格上没有蛇或梯子

相关信息

蛇与梯子游戏是一个经典的棋盘游戏，玩家通过掷骰子来决定移动的步数，棋盘上包含梯子和蛇，梯子可以直接将玩家带到棋盘上的一个更高级别，而蛇则将玩家带回低级别。

解题思路

1. 初始化：创建一个访问数组 vis 来记录每个格子是否被访问过，以及一个队列 queue 来存储当前正在处理的格子和到达该格子的步数。
2. 广度优先搜索（BFS）：使用队列来实现广度优先搜索。每次从队列中取出一个元素，这个元素包含当前格子的编号和到达这个格子的步数。
3. 探索下一步：对于每个可能的下一步（1到6），计算下一个格子的编号。如果这个格子有蛇或梯子，更新格子的编号。
4. 检查终点：如果到达终点，返回当前的步数。
5. 标记和扩展：如果下一个格子没有被访问过，将其标记为已访问，并将其加入队列中，步数加一。
6. 结束条件：如果队列变为空，说明无法到达终点，返回-1。
7. 辅助函数 id2rc：由于棋盘是对称的，这个函数用于将格子的编号转换为棋盘上的行列位置，并处理棋盘的左右对称性。

var snakesAndLadders = function (board) {
    // 棋盘的大小
    const n = board.length;
    // 创建一个访问数组，用于记录每个格子是否被访问过
    // 数组大小为 n*n + 1，因为棋盘上的格子是从1开始编号的
    const vis = new Array(n * n + 1).fill(0);
    // 创建一个队列，用于存储当前正在处理的格子和到达该格子的步数
    // 初始时，只有起点（编号1的格子）和步数0
    const queue = [[1, 0]];
    
    // 当队列不为空时，进行广度优先搜索
    while (queue.length) {
        // 从队列中取出一个元素，这个元素包含当前格子的编号和到达这个格子的步数
        const p = queue.shift();
        
        // 遍历每个可能的下一步（1到6）
        for (let i = 1; i <= 6; ++i) {
            // 计算下一个格子的编号
            let nxt = p[0] + i;
            // 如果超出边界，则跳出循环
            if (nxt > n * n) {
                break;
            }
            // 将格子的编号转换为棋盘上的行列位置
            const rc = id2rc(nxt, n);
            // 如果这个格子有蛇或梯子，更新格子的编号
            if (board[rc[0]][rc[1]] > 0) {
                nxt = board[rc[0]][rc[1]];
            }
            // 如果到达终点，返回当前的步数
            if (nxt === n * n) {
                return p[1] + 1;
            }
            // 如果下一个格子没有被访问过，将其标记为已访问，并将其加入队列中
            if (!vis[nxt]) {
                vis[nxt] = true;
                queue.push([nxt, p[1] + 1]); // 步数加一
            }
        }
    }
    // 如果无法到达终点，返回-1
    return -1;
};

// 辅助函数，用于将格子的编号转换为棋盘上的行列位置
const id2rc = (id, n) => {
    // 计算行和列
    let r = Math.floor((id - 1) / n), c = (id - 1) % n;
    // 由于棋盘是对称的，需要处理左右对称性
    if (r % 2 === 1) {
        c = n - 1 - c;
    }
    // 返回行列位置
    return [n - 1 - r, c];
}

最小基因变化（中）

基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。

假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。

• 例如，"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。

另有一个基因库 bank 记录了所有有效的基因变化，只有基因库中的基因才是有效的基因序列。（变化后的基因必须位于基因库 bank 中）

给你两个基因序列 start 和 end ，以及一个基因库 bank ，请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化，返回 -1 。

注意：起始基因序列 start 默认是有效的，但是它并不一定会出现在基因库中。

示例 1：

输入：start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出：1

示例 2：

输入：start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出：2

示例 3：

输入：start = "AAAAACCC", end = "AACCCCCC", bank = ["AAAACCCC","AAACCCCC","AACCCCCC"]
输出：3

提示：

• start.length == 8
• end.length == 8
• 0 <= bank.length <= 10
• bank[i].length == 8
• start、end 和 bank[i] 仅由字符 ['A', 'C', 'G', 'T'] 组成

解题思路

1. 理解问题: 首先明确，这是一个图论中的最短路径问题，其中基因是图的节点，如果两个基因之间可以通过一次变化相互转换，则它们之间有一条边。
2. 选择算法: 对于最短路径问题，广度优先搜索（BFS）是一个合适的选择，因为它可以在图中找到从起点到终点的最短路径。
3. 实现BFS:
   • 使用一个队列queue来存储待处理的基因和对应的变化次数。
   • 使用一个集合visited来存储已经访问过的基因，以避免重复访问。
   • 初始化队列，将起始基因和0（变化次数）加入队列。
   • 当队列不为空时，进行以下操作：
     • 从队列中取出一个基因和它的变化次数。
     • 如果这个基因是目标基因，则返回变化次数。
     • 否则，检查这个基因的所有可能的一次变化，并将新的基因和增加的变化次数加入队列（如果这个新的基因在基因库中且没有被访问过）。
4. 终止条件:
   • 如果找到目标基因，则返回当前的变化次数。
   • 如果队列变为空（即所有可能的路径都已被探索），且没有找到目标基因，则返回-1。
5. 注意事项:
   • 确保在每次变化后检查新的基因是否在基因库中。
   • 使用集合来跟踪已访问的基因，以优化性能并避免无限循环。

这个算法的关键在于使用BFS来保证找到的是最短路径，并且通过基因库来限制可能的路径，从而减少搜索空间。

var minMutation = function (startGene, endGene, bank) {
    let queue = [[startGene, 0]]; // 存储当前基因和变化次数
    let visited = new Set(); // 存储已经访问过的基因

    while (queue.length > 0) {
        let [currentGene, mutations] = queue.shift();
        
        if (currentGene === endGene) {
            return mutations; // 如果当前基因和目标基因相同，返回变化次数
        }

        for (let i = 0; i < currentGene.length; i++) {
            for (let char of ['A', 'C', 'G', 'T']) { // 基因的所有可能字符
                let newGene = currentGene.substring(0, i) + char + currentGene.substring(i + 1);
                if (!visited.has(newGene) && bank.includes(newGene)) {
                    visited.add(newGene);
                    queue.push([newGene, mutations + 1]); // 将新的基因和增加的变化次数加入队列
                }
            }
        }
    }

    return -1; // 如果没有找到路径，返回-1
};

单词接龙（难）

字典 wordList 中从单词 beginWord 到 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

• 每一对相邻的单词只差一个字母。
• 对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
• sk == endWord

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

提示：

• 1 <= beginWord.length <= 10
• endWord.length == beginWord.length
• 1 <= wordList.length <= 5000
• wordList[i].length == beginWord.length
• beginWord、endWord 和 wordList[i] 由小写英文字母组成
• beginWord != endWord
• wordList 中的所有字符串 互不相同

解题思路

image.png

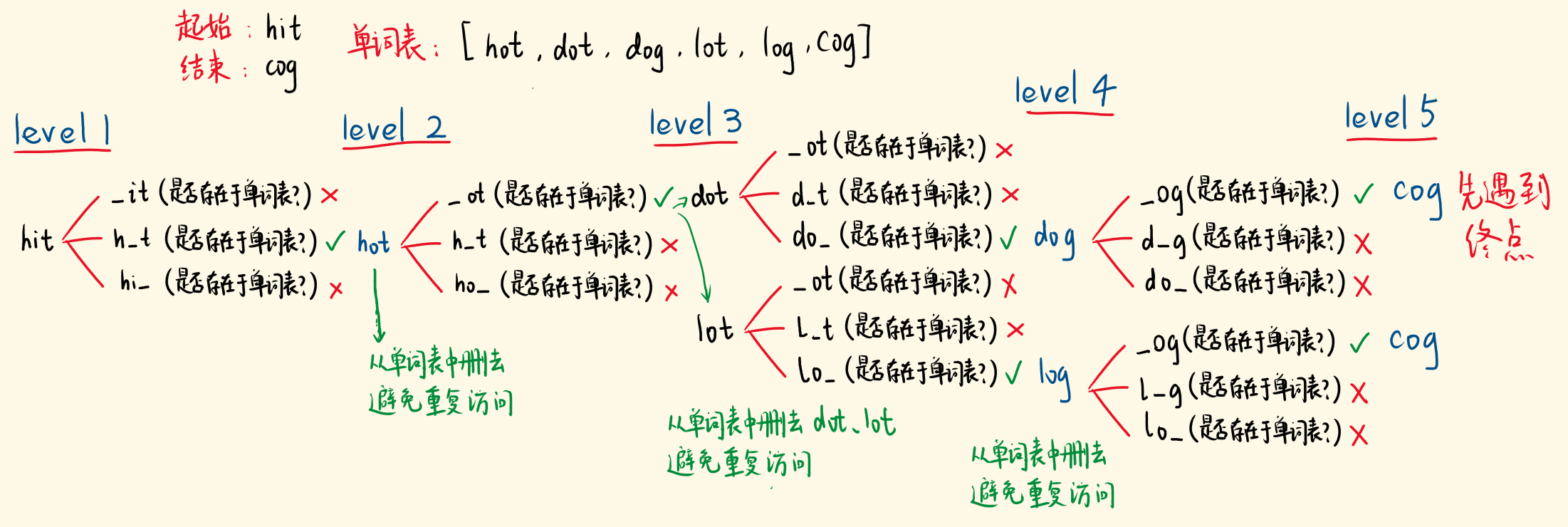
• 题意：从起点词出发，每次变一个字母，变换 n 次，变成终点词，希望 n 尽量小。
• 我们需要找出邻接关系，比如hit的转换词是 *it、h*t、hi*形式，看看这样的新词是否在单词表里，如果存在，就找到了一个下一层的转换词。
• 同时，要避免重复访问，hot->dot->hot，别这样变回来，徒增转换的次数。所以，确定了下一个转换词，就把它从单词表中删除。
• 下一层的转换词可能有多个，都要考察，哪一条转换路径先遇到终点词，它就最短。

整理一下

• 把单词看作结点，由一个结点带出下一层的邻接点，用BFS去做。
• 维护一个队列，让起点词入列，level 为 1，然后出列考察。
• 将逐个字符变成26字母之一，看看是否在单词表，如果在，该新词为下一层的转换词。
• 将它入列，它的 level +1，并从单词表中删去这个词。
• 出列、入列…重复，当出列的单词和终点词相同，就遇到了终点词，返回它的 level。
• 当队列为空时，代表考察完所有词，始终没有遇到终点词，没有路径通往终点。

const ladderLength = (beginWord, endWord, wordList) => {
    const wordSet = new Set(wordList);
    const queue = [];
    queue.push([beginWord, 1]);

    while (queue.length) {
        const [word, level] = queue.shift();  // 当前出列的单词
        if (word == endWord) {
            return level;
        }
        for (let i = 0; i < word.length; i++) { // 遍历当前单词的所有字符
            for (let c = 97; c <= 122; c++) { // 对应26个字母
                const newWord = word.slice(0, i) + String.fromCharCode(c) + word.slice(i + 1); // 形成新词
                if (wordSet.has(newWord)) { // 单词表里有这个新词
                    queue.push([newWord, level + 1]); // 作为下一层的词入列
                    wordSet.delete(newWord);  // 避免该词重复入列
                }
            }
        }
    }
    return 0; // bfs结束，始终没有遇到终点
};