案例
...大约 10 分钟
实现 Trie (前缀树)(中)
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie()初始化前缀树对象。void insert(String word)向前缀树中插入字符串word。boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。boolean startsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
提示:
1 <= word.length, prefix.length <= 2000word和prefix仅由小写英文字母组成insert、search和startsWith调用次数 总计 不超过3 * 104次
解题思路
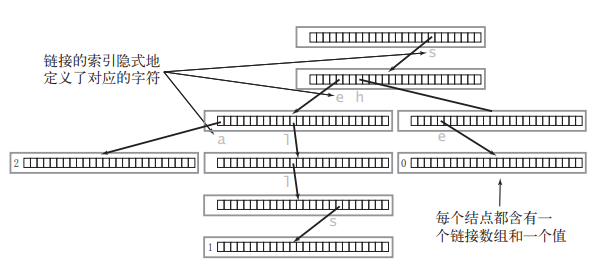
想象以下,包含三个单词 "sea","sells","she" 的 Trie 会长啥样呢?
它的真实情况是这样的:
// 定义Trie类
var Trie = function() {
// 初始化一个空的children对象,用于存储子节点
this.children = {};
};
// 向Trie中插入一个单词
Trie.prototype.insert = function(word) {
// 从根节点的children开始
let node = this.children;
// 遍历单词中的每个字符
for (const ch of word) {
// 如果当前字符不在node中,创建一个新对象作为其子节点
if (!node[ch]) {
node[ch] = {};
}
// 移动到下一个字符对应的节点
node = node[ch];
}
// 在单词的最后一个字符节点上设置isEnd标记,表示这是一个单词的结束
node.isEnd = true;
};
// 搜索前缀,返回前缀的最后一个字符对应的节点
Trie.prototype.searchPrefix = function(prefix) {
// 从根节点的children开始
let node = this.children;
// 遍历前缀中的每个字符
for (const ch of prefix) {
// 如果当前字符不在node中,表示前缀不存在,返回false
if (!node[ch]) {
return false;
}
// 移动到下一个字符对应的节点
node = node[ch];
}
// 前缀存在,返回最后一个字符对应的节点
return node;
}
// 搜索整个单词
Trie.prototype.search = function(word) {
// 使用searchPrefix函数搜索单词
const node = this.searchPrefix(word);
// 检查单词是否存在:节点必须存在,且isEnd标记必须为true
return node !== undefined && node.isEnd !== undefined;
};
// 检查是否存在以给定前缀开头的单词
Trie.prototype.startsWith = function(prefix) {
// 直接使用searchPrefix函数,因为只要前缀存在,就返回true
return this.searchPrefix(prefix);
};
添加与搜索单词 - 数据结构设计(中)
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
WordDictionary()初始化词典对象void addWord(word)将word添加到数据结构中,之后可以对它进行匹配bool search(word)如果数据结构中存在字符串与word匹配,则返回true;否则,返回false。word中可能包含一些'.',每个.都可以表示任何一个字母。
示例:
输入:
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
输出:
[null,null,null,null,false,true,true,true]
解释:
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // 返回 False
wordDictionary.search("bad"); // 返回 True
wordDictionary.search(".ad"); // 返回 True
wordDictionary.search("b.."); // 返回 True
提示:
1 <= word.length <= 25addWord中的word由小写英文字母组成search中的word由 '.' 或小写英文字母组成- 最多调用
104次addWord和search
解题思路
该算法是基于字典树(Trie)的单词查找。字典树是一种树形数据结构,用于存储一组字符串,支持快速查找和插入操作。下面是这个算法的解题思路总结:
- 字典树的构建(
addWord方法)
- 初始化:字典树的每个节点都有一个子节点集合(
children),初始为空。 - 添加单词:对于每个单词,从根节点开始,逐个字符遍历单词。
- 如果当前字符在子节点集合中不存在,则创建一个新的子节点。
- 移动到下一个字符,直到单词的最后一个字符。
- 在最后一个字符的节点上标记
isEnd,表示这是一个单词的结尾。
- 单词搜索(
search方法)
- 初始化:从根节点开始搜索。
- 递归搜索:对于单词中的每个字符,根据字符类型进行不同的处理。
- 普通字符:如果字符在当前节点的子节点中存在,则继续递归搜索下一个字符。
- 通配符(
.):遍历当前节点的所有子节点,对每个子节点递归搜索。如果任何路径返回true,整个搜索返回true。 - 如果字符不在子节点中,或者所有路径都失败,返回
false。
- 搜索终止条件
- 当搜索到单词的最后一个字符时,检查当前节点是否被标记为
isEnd。 - 如果是,返回
true,表示找到了单词。 - 如果不是,返回
false。
- 整体逻辑
addWord方法用于构建字典树,支持快速添加和存储单词。search方法用于在字典树中搜索单词,支持普通字符和通配符的搜索。- 通过递归遍历字典树,
search方法能够高效地处理包含通配符的复杂搜索查询。
这个算法的关键在于字典树的结构,它使得单词的添加和搜索操作都非常高效。特别是对于通配符搜索,通过递归遍历所有可能的路径,算法能够找到所有匹配的单词。
var WordDictionary = function () {
this.children = {}
};
WordDictionary.prototype.addWord = function (word) {
let node = this.children;
for (let ch of word) {
if (!node[ch]) {
node[ch] = {}
}
node = node[ch]
}
node.isEnd = true
};
// WordDictionary类的search方法
WordDictionary.prototype.search = function (word) {
// 从根节点开始搜索
return this._searchInNode(this.children, word, 0);
};
// 辅助递归搜索函数
WordDictionary.prototype._searchInNode = function (node, word, index) {
// 如果索引到达单词的末尾,检查当前节点是否标记为单词的结尾
if (index === word.length) {
return node.isEnd === true;
}
// 获取单词中当前索引的字符
const ch = word[index];
// 如果字符是'.', 遍历所有子节点
if (ch === '.') {
for (const child in node) {
// 确保child是node的直接属性,而不是原型链上的属性
if (node.hasOwnProperty(child) && this._searchInNode(node[child], word, index + 1)) {
// 如果任何子节点的递归搜索返回true,整个搜索返回true
return true;
}
}
// 如果所有子节点的递归搜索都返回false,整个搜索返回false
return false;
} else {
// 如果字符不是'.',直接递归到相应的子节点
if (!node[ch]) return false;
return this._searchInNode(node[ch], word, index + 1);
}
};
单词搜索 II(难)
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words, 返回所有二维网格上的单词 。
单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例 1:

输入:board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出:["eat","oath"]
示例 2:
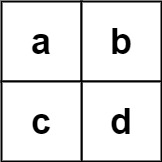
输入:board = [["a","b"],["c","d"]], words = ["abcb"]
输出:[]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]是一个小写英文字母1 <= words.length <= 3 * 1041 <= words[i].length <= 10words[i]由小写英文字母组成words中的所有字符串互不相同
解题思路
- Trie(前缀树)的构建:首先,我们构建一个Trie,用于存储所有需要查找的单词。Trie是一种树形结构,用于高效地存储和检索字符串数据集中的键。每个节点包含一个字符和指向子节点的指针。
- 深度优先搜索(DFS):然后,我们使用深度优先搜索算法遍历字符矩阵。从每个字符开始,我们检查当前字符是否存在于Trie的当前节点中。如果存在,我们继续搜索该字符的相邻字符。
- 单词查找与标记:在搜索过程中,如果我们在Trie中找到一个完整的单词,我们就将其添加到结果集中,并从Trie中移除,以避免重复。同时,我们用
'#'字符标记已访问的矩阵位置,以避免在搜索中重复访问。 - 清理Trie:在搜索完成后,如果Trie中的某个节点不再需要(即它的所有子节点都已被访问),我们将其从Trie中删除,以减少内存使用。
这个算法的关键在于Trie数据结构的运用,它使得单词的查找和匹配非常高效。通过DFS遍历矩阵并结合Trie,我们能够有效地找到矩阵中所有出现的单词。
dfs 中为什么要撤销对当前位置的标记?
在深度优先搜索(DFS)算法中,恢复当前位置(即撤销对当前位置的标记)是非常重要的,原因如下:
- 避免影响其他路径:在DFS中,我们可能会从多个方向探索当前位置的相邻位置。如果不恢复当前位置,那么在探索其他路径时,我们可能会错误地认为这个位置已经被访问过,从而影响搜索的正确性。
- 保持矩阵的原始状态:在搜索过程中,我们可能需要多次访问同一个位置,尤其是在不同的搜索路径上。如果不恢复位置,矩阵的状态就会随着搜索的进行而改变,这可能导致错误的结果。
- 允许重复使用字符:在某些情况下,同一个字符可能在多个单词中出现,或者在同一个单词中被多次使用(例如,如果单词在矩阵中弯曲或重叠)。恢复位置确保了我们可以重复使用矩阵中的字符。
- 简化逻辑:恢复位置使得DFS算法的逻辑更加简单和直观。我们不需要为已访问的位置维护一个单独的数据结构,只需在每次递归调用返回时恢复当前位置即可。
总之,恢复当前位置是DFS算法中的一个重要步骤,它确保了算法的正确性和效率,同时简化了代码的实现。
// TrieNode类用于构建Trie树
class TrieNode {
constructor() {
this.children = new Map();
this.word = null;
}
}
// Trie类用于插入单词和查找单词
class Trie {
constructor() {
this.root = new TrieNode();
}
insert(word) {
let current = this.root;
for (let char of word) {
if (!current.children.has(char)) {
current.children.set(char, new TrieNode());
}
current = current.children.get(char);
}
current.word = word; // 存储单词
}
}
// 方向数组,用于在矩阵中上下左右移动
const dirs = [[1, 0], [-1, 0], [0, 1], [0, -1]];
// 深度优先搜索函数
function dfs(node, board, i, j, ans) {
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) return;
const ch = board[i][j];
if (!node.children.has(ch)) return;
node = node.children.get(ch);
if (node.word !== null) {
ans.add(node.word);
node.word = null; // 避免重复添加单词
}
board[i][j] = '#'; // 标记当前位置已访问
for (const [dx, dy] of dirs) {
dfs(node, board, i + dx, j + dy, ans);
}
board[i][j] = ch; // 恢复当前位置
}
var findWords = function (board, words) {
const trie = new Trie();
for (const word of words) {
trie.insert(word);
}
const ans = new Set();
for (let i = 0; i < board.length; ++i) {
for (let j = 0; j < board[0].length; ++j) {
dfs(trie.root, board, i, j, ans);
}
}
return Array.from(ans);
};
Powered by Waline v3.3.0