案例
删除排序数组中的重复项(简)
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素应该保存最终结果。
将最终结果插入 nums 的前 k 个位置后返回 k 。
不要使用额外的空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
解题思路
双指针思想:
- 定义两个指针分别代表数组第一个和第二个索引;
- 如果左指针指向的元素和右指针一样,那么就让右指针往右移动一位;
- 如果左右指针指向的元素不一样,那么就让左指针向右移动一位,并且将左指针指向元素值改成右指针指向的元素值;
- 重复2、3两步,直到右指针指向最后一个元素;
- 最后删除左指针后面的元素即可;
// 定义一个函数 removeDuplicates,接收一个数组 nums 作为参数
var removeDuplicates = function(nums) {
// 初始化两个指针 R 和 L,分别表示右指针和左指针,初始位置都为数组的第一个元素
let R = 0, L = 0;
// 当右指针 R 小于数组长度时,执行循环
while (R < nums.length) {
// 检查右指针所指元素是否与左指针所指元素相等
if (nums[R] != nums[L]) {
// 如果不相等,将左指针向右移动一位
L++;
// 更新左指针位置上的元素为右指针所指元素,实现去重
nums[L] = nums[R];
}
// 右指针向右移动一位
R++;
}
// 返回去重后的数组长度,即左指针位置加 1
return L + 1;
};
买卖股票的最佳时机 ||(简)
给定一个数组 prices ,其中 prices[i] 表示股票第 i 天的价格。
在每一天,你可能会决定购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以购买它,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
解题思路
这道题用贪心算法解决最为简单。那什么是贪心算法呢?
指的就是在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
那么我们只要每次在股票上涨前买入就可以得到最大收益,所以只要算出每次上涨的差额,再进行累加就可以了。
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function(prices) {
let i = 0;
let j = 1;
let result = 0;
while(j <= prices.length) {
if(prices[i] < prices[j]) {
result += (prices[j] - prices[i])
}
i++;
j++;
}
return result;
};
旋转数组(简)
给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
解题思路
通过观察发现,其实轮转的结果无非就只有两种情况:
当 k 的值小于数组的长度时,轮转后的数组就是将数组的后 k 位移动至数组的最前面;
当 k 的值大于数组的长度时,如果 k 正好时数组长度的倍数,那么轮转后还是原始数组;如果不是,那么就轮转 k 除以数组长度的余数次,这时余数的值必然是小于数组的长度的,直接使用第一种情况的逻辑即可。
结合 es6 的语法,可以将代码精简至两行:
/**
* @param {number[]} nums
* @param {number} k
* @return {void} Do not return anything, modify nums in-place instead.
*/
var rotate = function(nums, k) {
const v = k % nums.length;
return nums.unshift(...nums.splice(-v,v))
}
存在重复元素(简)
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1]
输出:true
示例 2:
输入:nums = [1,2,3,4]
输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2]
输出:true
解题思路
利用 es6 的 set 数据结构进行数组去重,然后和原始数组比较长度即可。
/**
* @param {number[]} nums
* @return {boolean}
*/
var containsDuplicate = function(nums) {
const set = new Set(nums);
if(set.size < nums.length) {
return true;
} else {
return false;
}
};
只出现一次的数字(简)
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
解题思路
按位异或赋值 (^=)
按位异或赋值操作符 (^=) 使用二进制表示操作数,进行一次按位异或操作并赋值。
- 如果两个数一样,进行异或操作就是0。
- 0和任何数进行异或操作都会变成和它异或的对象。
/**
* @param {number[]} nums
* @return {number}
*/
var singleNumber = function(nums) {
return nums.reduce((a,b) => a ^ b)
};
两个数组的交集 ||(简)
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[4,9]
方法一
Map 思想:
- 使用一个 hash 表记录其中一个数组每个元素出现的次数
- 然后遍历第二个数组,如果 map 对应 key 的值大于 0,则放入返回数组中,然后让 map 对应 key 的值减 1
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var intersect = function (nums1, nums2) {
const res = [];
const map = {}
for (let i of nums1) {
if (map[i]) {
map[i]++
} else {
map[i] = 1
}
}
for (let j of nums2) {
if (map[j] > 0) {
res.push(j)
map[j]--
}
}
return res
};
方法二
双指针思想:
- 首先对两个数组进行从小到大排序;
- 接着分别让一个指针指向两个数组的第一位;
- 如果两个指针指向的元素相同,说明是交集,将其值存入结果数组,随后两个指针都后移一位;
- 如果两个指针指向的元素不同,让指向的值值相对小的往后移一位,因为数组是从小到大排序的,如果大的后移可能会丢失相交集的元素;相对大的先不动;
- 一直重复3、4两步即可。
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var intersect = function(nums1, nums2) {
nums1.sort((a, b) => a - b);
nums2.sort((a, b) => a - b); // 为了使相同元素相邻出现
let i = 0;
let j = 0;
let result = []
while(i < nums1.length && j < nums2.length) {
if(nums1[i] === nums2[j]) {
result.push(nums1[i])
i++;
j++;
} else if(nums1[i] < nums2[j]) {
i ++;
} else {
j ++;
}
}
return result;
};
加一(简)
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
示例 2:
输入:digits = [4,3,2,1]
输出:[4,3,2,2]
解释:输入数组表示数字 4321。
示例 3:
输入:digits = [0]
输出:[1]
解题思路
- 主要考虑进位的问题
- 从数组尾部开始便利
/**
* @param {number[]} digits
* @return {number[]}
*/
var plusOne = function(digits) {
for(let i = digits.length - 1; i >= 0;i--) {
digits[i]++; // 尾部加一
digits[i] %= 10; // 判断最后一位是否是9
if(digits[i] !== 0) return digits; // 如果没有进位,直接返回数组
}
return [1,...digits] // 如果for循环里没有return,说明每一位都是 9,位数加一
};
移动零(简)
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
解题思路
- 一开始想到的是,遍历数组,然后将等于 0 的元素依次放到后面
- 然后看了解题,直接用 es6 的 sort 一行代码就能搞定
/**
* @param {number[]} nums
* @return {void} Do not return anything, modify nums in-place instead.
*/
var moveZeroes = function(nums) {
if(nums.length < 2) return;
let i = 0;
let j = nums.length;
while(i < j) {
if(nums[i] === 0) {
nums.splice(i,1);
nums.push(0);
j--;
} else {
i ++;
}
}
};
// sort 版本
var moveZeroes = function(nums) {
return nums.sort((a,b) => b ? 0 : -1)
};
两数之和(简)
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
解题思路
- 双层for循环暴力破解
- map 哈希表优化
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
// 暴力破解
var twoSum = function(nums, target) {
for(let i = 0;i < nums.length - 1;i++) {
for(let j = i + 1; j < nums.length; j++) {
if(nums[i] + nums[j] === target) {
return [i,j]
}
}
}
};
// hash表
var twoSum = function(nums, target) {
let map = new Map();
for(let i = 0; i < nums.length;i++) {
let other = target - nums[i]
if(map.has(other)) {
return [i,map.get(other)]
} else {
map.set(nums[i],i)
}
}
};
多数元素(简)
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
提示
- n == nums.length
- 1 <= n <= 5 * 104
- -109 <= nums[i] <= 109
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
解题思路
利用 hash 表记录每个元素出现的次数,当有元素的次数大于 n / 2 时,直接返回
/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function (nums) {
let map = new Map();
const len = nums.length;
for (const i of nums) {
if (map.has(i)) {
let temp = map.get(i);
map.set(i, ++temp);
if (temp > len / 2) return i;
} else {
// 只有一个元素直接返回
if (len === 1) return i;
map.set(i, 1);
}
}
};
找到所有数组中消失的数字(简)
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
示例 1:
输入:nums = [4,3,2,7,8,2,3,1]
输出:[5,6]
示例 2:
输入:nums = [1,1]
输出:[2]
提示
- n == nums.length
- 1 <= n <= 105
- 1 <= nums[i] <= n
进阶:你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。
解题思路
- 暴力破解
/**
* @param {number[]} nums
* @return {number[]}
*/
var findDisappearedNumbers = function (nums) {
const arr = [];
const len = nums.length;
for (let i = 1; i <= len; i++) {
if (!nums.includes(i)) {
arr.push(i);
}
}
return arr
};
数组中不等三元组的数目(简)
给你一个下标从 0 开始的正整数数组 nums 。请你找出并统计满足下述条件的三元组 (i, j, k) 的数目:
0 <= i < j < k < nums.length
nums[i]、nums[j] 和 nums[k] 两两不同 。
换句话说:nums[i] != nums[j]、nums[i] != nums[k] 且 nums[j] != nums[k] 。
返回满足上述条件三元组的数目。
示例 1:
输入:nums = [4,4,2,4,3]
输出:3
解释:下面列出的三元组均满足题目条件:
- (0, 2, 4) 因为 4 != 2 != 3
- (1, 2, 4) 因为 4 != 2 != 3
- (2, 3, 4) 因为 2 != 4 != 3
共计 3 个三元组,返回 3 。
注意 (2, 0, 4) 不是有效的三元组,因为 2 > 0 。
示例 2:
输入:nums = [1,1,1,1,1]
输出:0
解释:不存在满足条件的三元组,所以返回 0 。
提示
- 3 <= nums.length <= 100
- 1 <= nums[i] <= 1000
解题思路
因为数组的长度最大是100,可以直接暴力枚举
这段代码是一个JavaScript函数,它的名字叫做"unequalTriplets"。参数是一个名为"nums"的数组。下面是函数的解释:
调用数组的.sort()方法,将数组中的内容从小到大排序,以方便后续操作。
定义了两个变量res和n,其中res表示结果,n表示数组的长度。
进入一个for循环,循环的条件是i小于n,每次循环结束后,i=j。这个循环用于处理数组中相同的元素。
在每次循环的开始,有一个while循环,其条件是j小于n并且数组中的第j个元素等于第i个元素。这个while循环用于找到所有与第i个元素相等的元素。
循环结束时,将res加上i * (j - i) * (n - j),其中i表示与第i个元素相等的元素的个数,j-i表示与第i个元素相等的元素跨度,n-j表示不等于第i个元素的元素的个数。
最终返回res作为结果。
在第五步,代码计算了一个res的值,这个值代表着数组中三元组的个数,其中每个三元组都不相同。具体的解释如下:
- i代表数组中与当前元素nums[i]相等的元素个数。
- (j-i)表示当前元素与第一个不相等的元素之间跨越的元素个数。
- (n-j)表示当前元素之后、与当前元素不相等的元素个数。
- i * (j-i) * (n-j)表示以当前元素作为最小值形成的三元组的个数。因为三元组中最小的数必须是nums[i],而与nums[i]相等的数有i个,最小的数后面跨越的元素个数为j-i,其后的元素个数为n-j,它们构成的三元组个数是i*(j-i)*(n-j)。
因此,通过这个公式,代码计算出每个元素作为最小值时形成的三元组个数,把它们加起来,最后就得到了结果。注意,这个算法前提是数组中没有重复元素,否则可能会出现重复计算的问题。
var unequalTriplets = function(nums) {
let res = 0, n = nums.length;
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
for (let k = j + 1; k < n; k++) {
if (nums[i] != nums[j] && nums[i] != nums[k] && nums[j] != nums[k]) {
res++;
}
}
}
}
return res;
};
var unequalTriplets = function(nums) {
nums.sort();
let res = 0, n = nums.length;
for (let i = 0, j = 0; i < n; i = j) {
while (j < n && nums[j] == nums[i]) {
j++;
}
res += i * (j - i) * (n - j);
}
return res;
};
合并两个有序数组(简)
题目描述
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
**注意:**最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
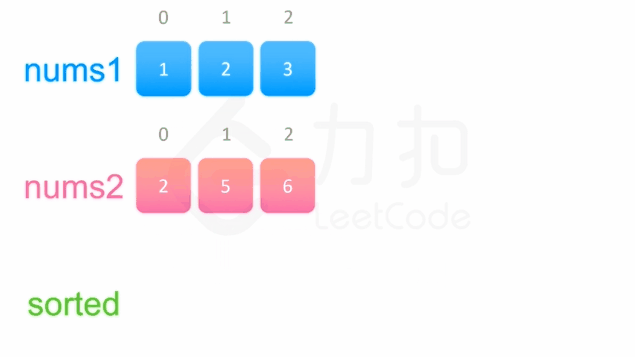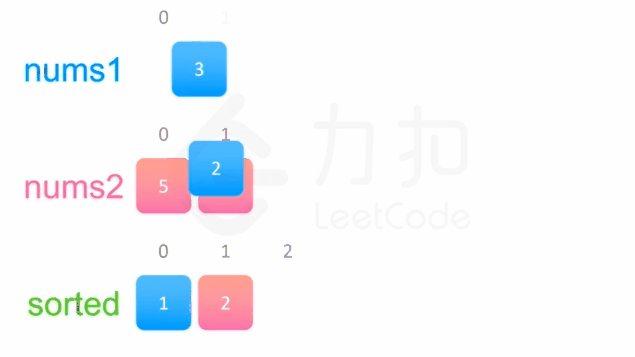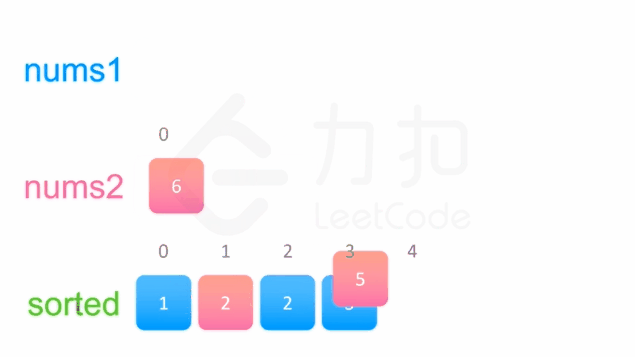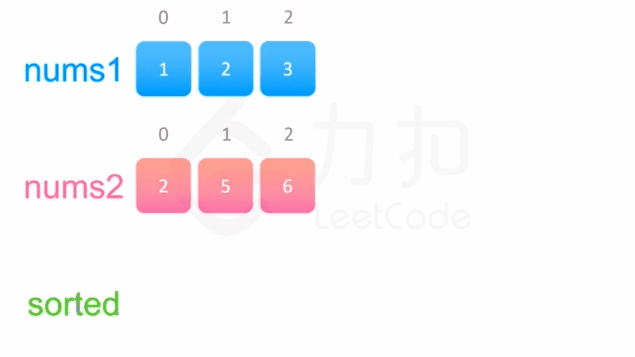
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
self
解题思路
因为数组是有序的,所以只要遍历 nums2 数组中的元素,然后插入到 nums1 中,关键就是找到插入的位置,分为两种情况:
- 寻找到 nums1 中第一个大于当前 nums2 元素的索引,那么直接插入即可
- 如果找不到大于当前元素的值,则将当前元素插入到末尾
需要注意的是:需要初始化一个指针,指向 nums1 数组的末尾有效元素
// 定义合并函数,将两个有序数组合并到第一个数组中
var merge = function(nums1, m, nums2, n) {
// 初始化指针 t,指向 nums1 数组的末尾有效元素
let t = m - 1;
// 遍历 nums2 数组中的每个元素
nums2.forEach(item => {
// 移除 nums1 数组末尾的元素
nums1.pop();
// 将指针 t 后移一位
t++;
// 寻找 nums1 中第一个大于当前 nums2 元素的索引
const rIndex = nums1.findIndex(i => item < i);
// 如果找不到大于当前元素的值,则将当前元素插入到末尾
const index = rIndex === -1 ? t : rIndex;
// 在 nums1 数组的指定索引处插入当前元素
nums1.splice(index, 0, item);
});
};
有什么不足
使用 pop 和 splice 来删除和插入元素,这样的操作会导致数组重新排序,影响性能。
方法一:直接合并后排序
解题思路
最直观的方法是先将数组 nums2 放进数组 nums1 的尾部,然后直接对整个数组进行排序。
var merge = function (nums1, m, nums2, n) {
nums1.splice(m, n, ...nums2);
nums1.sort((a, b) => a - b)
};
方法二:双指针法
解题思路
- 初始化两个指针,分别指向nums1和nums2 的头部
- 创建一个新数组用于存放合并后的结果
- 因为数组是有序的,所以每次对比nums1和nums2头部元素的大小,然后依次插入到结果数组中即可
- 最后将结果数组中的元素依次复制给 nums1 即可
// 合并两个有序数组
var merge = function(nums1, m, nums2, n) {
// 初始化两个指针,分别指向nums1和nums2
let p1 = 0, p2 = 0;
// 创建一个新数组用于存放合并后的结果
const sorted = new Array(m + n).fill(0);
// 当前元素的变量
var cur;
while (p1 < m || p2 < n) {
// 如果nums1的元素已经全部遍历完,将nums2的当前元素加入结果数组
if (p1 === m) {
cur = nums2[p2++];
}
// 如果nums2的元素已经全部遍历完,将nums1的当前元素加入结果数组
else if (p2 === n) {
cur = nums1[p1++];
}
// 如果nums1的当前元素小于nums2的当前元素,将nums1的当前元素加入结果数组
else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
}
// 否则,将nums2的当前元素加入结果数组
else {
cur = nums2[p2++];
}
// 将当前元素加入结果数组
sorted[p1 + p2 - 1] = cur;
}
// 将排序好的数组复制回原数组nums1
for (let i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
};
方法三:逆向双指针
解题思路
方法二中,之所以要使用临时变量,是因为如果直接合并到数组 nums1 中,nums1 中的元素可能会在取出之前被覆盖。那么如何直接避免覆盖 numsr 中的元素呢?观察可知,nums1 的后半部分是空的,可以直接覆盖而不会影响结果。因此可以指针设置为从后向前遍历,每次取两者之中的较大者
放进 nums1 的最后面。
// 合并两个有序数组的函数
var merge = function(nums1, m, nums2, n) {
// 初始化指针,p1指向nums1的末尾(有效元素的最后一个位置),p2指向nums2的末尾
let p1 = m - 1, p2 = n - 1;
// 初始化合并后数组的末尾位置
let tail = m + n - 1;
var cur; // 用于存储当前比较的元素的变量
// 循环,直到p1和p2都小于0
while (p1 >= 0 || p2 >= 0) {
// 如果p1已经小于0,说明nums1的元素都已经遍历完
if (p1 === -1) {
cur = nums2[p2--]; // 将nums2的当前元素放入合并后数组,同时移动p2指针
}
// 如果p2已经小于0,说明nums2的元素都已经遍历完
else if (p2 === -1) {
cur = nums1[p1--]; // 将nums1的当前元素放入合并后数组,同时移动p1指针
}
// 如果nums1[p1]大于nums2[p2],将nums1[p1]放入合并后数组
else if (nums1[p1] > nums2[p2]) {
cur = nums1[p1--]; // 同时移动p1指针
}
// 如果nums2[p2]大于等于nums1[p1],将nums2[p2]放入合并后数组
else {
cur = nums2[p2--]; // 同时移动p2指针
}
nums1[tail--] = cur; // 将当前比较得到的元素放入合并后数组的末尾
}
};
移除元素(简)
题目描述
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以**「引用」**方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,3,0,4]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
提示:
0 <= nums.length <= 1000 <= nums[i] <= 500 <= val <= 100
self
// 定义名为 removeElement 的函数,用于移除数组中指定的元素
var removeElement = function(nums, val) {
// 使用 for 循环遍历数组中的每个元素
for (let i = 0; i < nums.length;) {
// 检查当前元素是否等于指定的值 val
if (nums[i] === val) {
// 如果相等,使用 splice 方法移除当前位置的元素
nums.splice(i, 1);
// 使用 continue 关键字跳过当前循环的剩余代码,直接进入下一次循环
continue;
}
// 如果当前元素不等于指定值,增加循环变量 i,继续下一次循环
i++;
}
};
有什么问题
在循环中修改数组的长度可能会导致索引混乱。
双指针法
解题思路
- 初始化左右指针,分别指向数组的起始位置和末尾位置
- 如果左指针指向的元素等于要移除的值val,将左指针指向的元素替换为右指针指向的元素,并将右指针向左移动
- 如果左指针指向的元素不等于要移除的值val,则将左指针向右移动
- 循环结束后,返回左指针的值,即移除元素后的新数组长度
// 定义名为removeElement的函数,接收两个参数:nums(数组)和val(要移除的元素)
var removeElement = function (nums, val) {
// 初始化左指针为数组的起始位置
let left = 0;
// 初始化右指针为数组的末尾位置
let right = nums.length - 1;
// 当左指针小于等于右指针时,执行循环
while(left <= right) {
// 如果左指针指向的元素等于要移除的值val
if(nums[left] === val) {
// 将左指针指向的元素替换为右指针指向的元素,并将右指针向左移动
nums[left] = nums[right--];
} else {
// 如果左指针指向的元素不等于要移除的值val,则将左指针向右移动
left++;
}
}
// 循环结束后,返回左指针的值,即移除元素后的新数组长度
return left;
};
买卖股票的最佳时机(简)
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
法一:暴力破解法
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function (prices) {
let max = 0
for (let i = 0; i < prices.length; i++) {
for (let j = i + 1; j < prices.length; j++) {
const profit = prices[j] - prices[i];
if(profit > max) {
max = profit
}
}
}
return max
};
法二:一次遍历
提示
我们来假设自己来购买股票。随着时间的推移,每天我们都可以选择出售股票与否。那么,假设在第 i 天,如果我们要在今天卖股票,那么我们能赚多少钱呢?
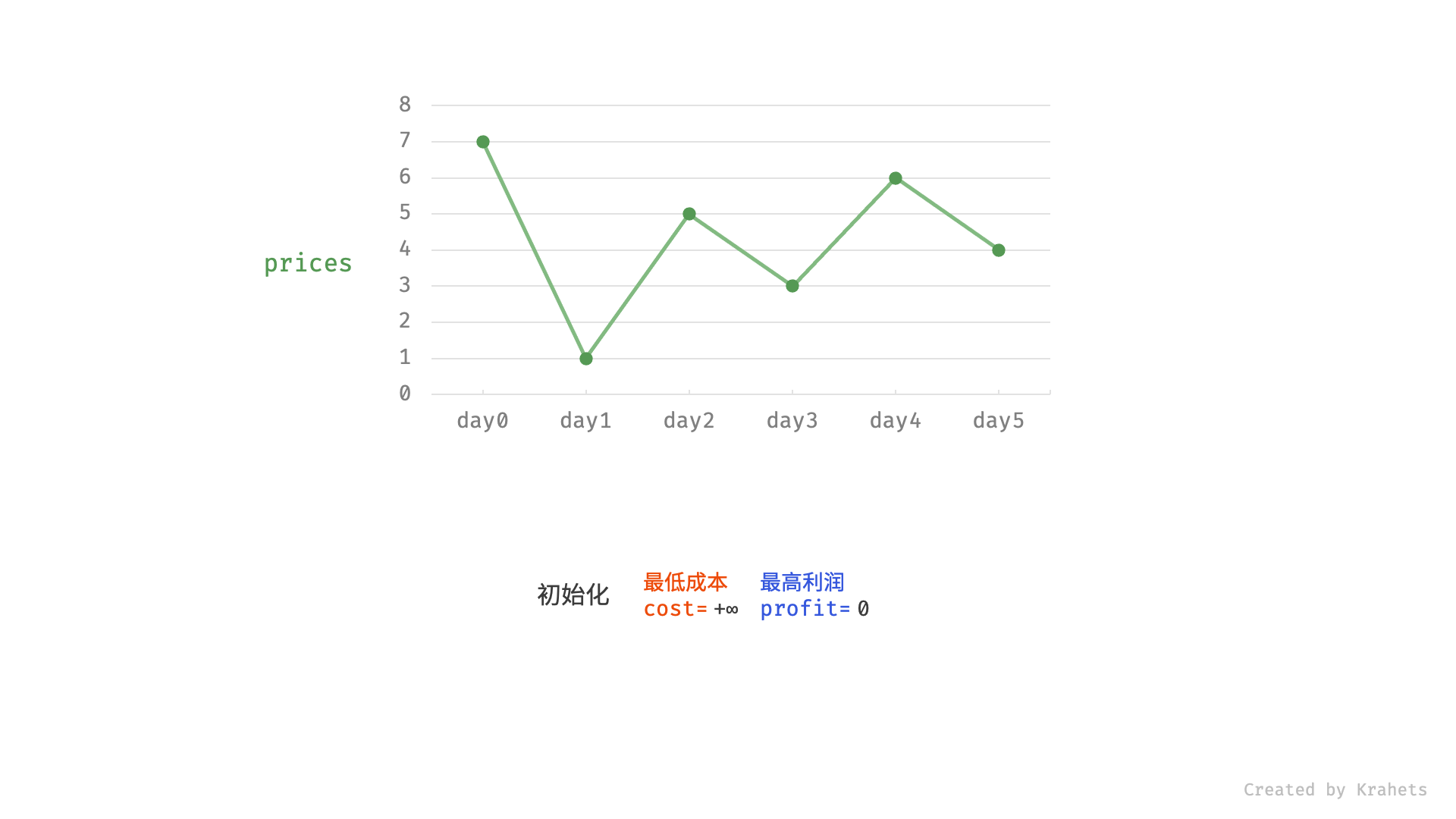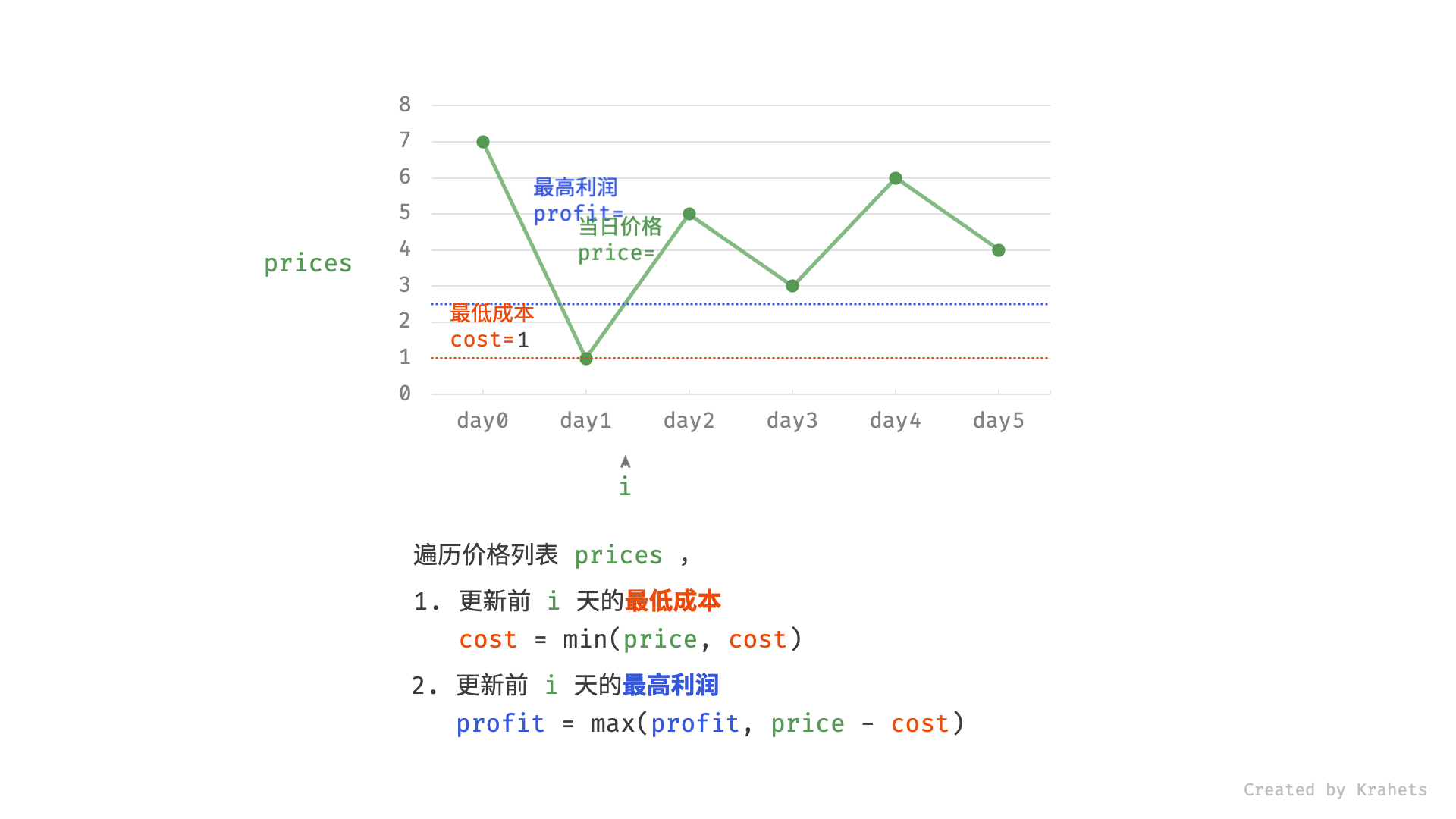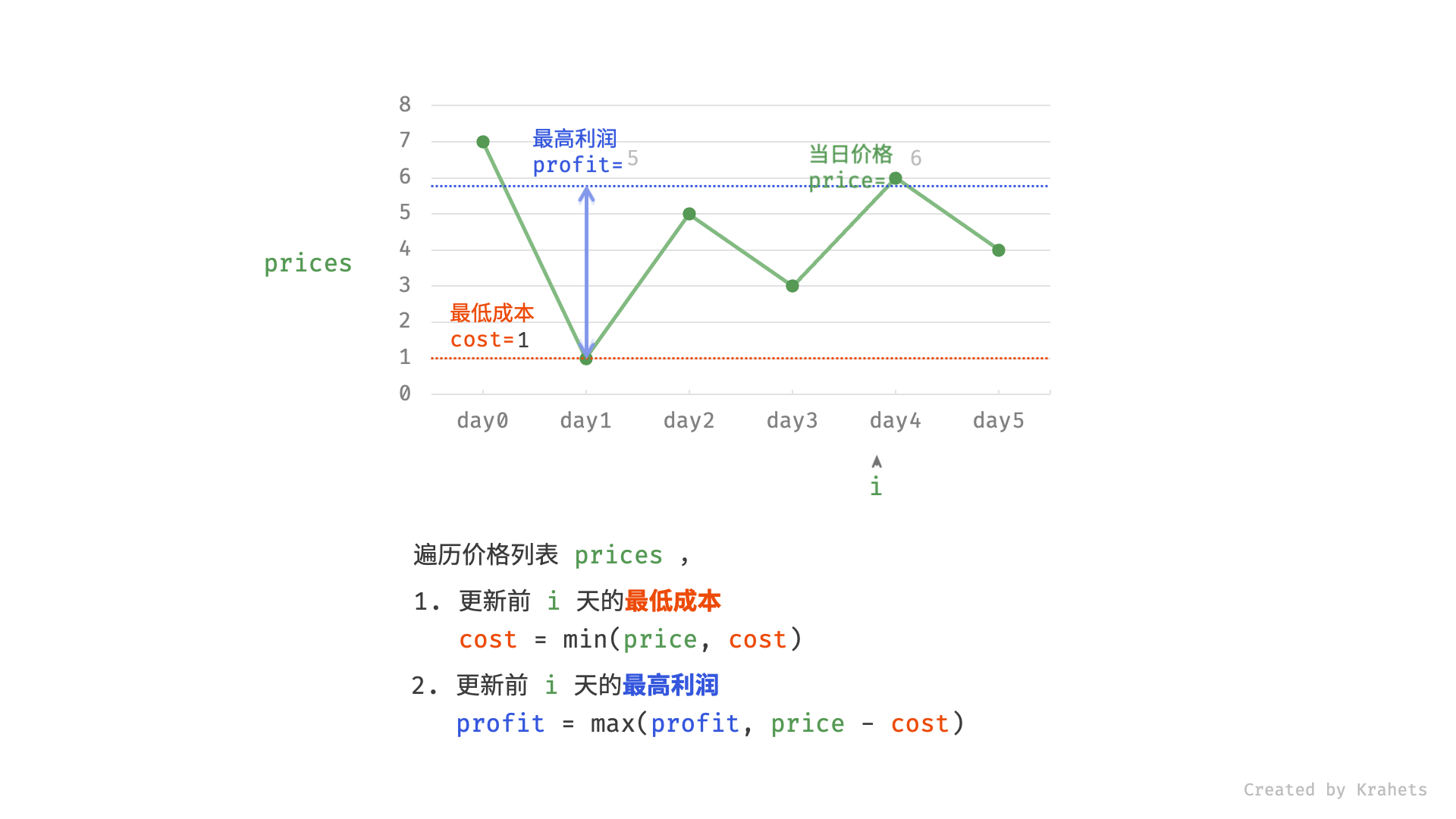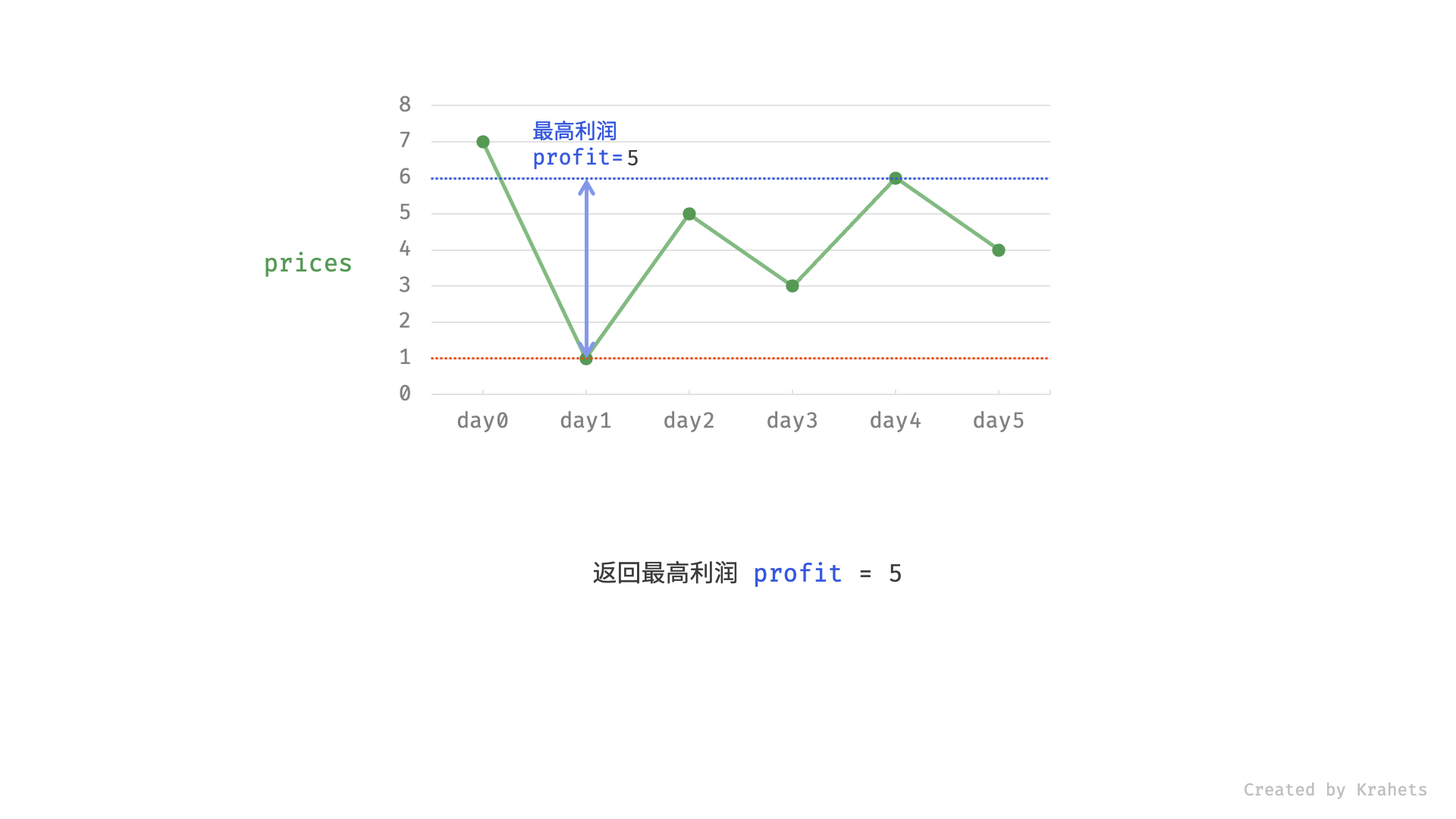
显然,如果我们真的在买卖股票,我们肯定会想:如果我是在历史最低点买的股票就好了!太好了,在题目中,我们只要用一个变量记录一个历史最低价格 minprice,我们就可以假设自己的股票是在那天买的。那么我们在第 i 天卖出股票能得到的利润就是 prices[i] - minprice。
因此,我们只需要遍历价格数组一遍,记录历史最低点,然后在每一天考虑这么一个问题:如果我是在历史最低点买进的,那么我今天卖出能赚多少钱?当考虑完所有天数之时,我们就得到了最好的答案。
// 定义一个名为maxProfit的函数,接受一个参数prices(代表股票价格数组)
var maxProfit = function (prices) {
// 初始化最小价格为JavaScript中的最大数值
let minPrice = Number.MAX_VALUE;
// 初始化最大利润为0
let maxProfit = 0;
// 遍历股票价格数组
for (let i = 0; i < prices.length; i++) {
// 如果当前价格小于最小价格
if (prices[i] < minPrice) {
// 更新最小价格为当前价格
minPrice = prices[i];
}
// 如果当前价格减去最小价格大于当前最大利润
else if (prices[i] - minPrice > maxProfit) {
// 更新最大利润为当前价格减去最小价格
maxProfit = prices[i] - minPrice;
}
}
// 返回最大利润
return maxProfit;
};
删除排序数组中的重复项 II(简)
给你一个有序数组 nums ,请你** 原地** 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以**「引用」**方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [1,1,1,2,2,3]
输出:5, nums = [1,1,2,2,3]
解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,1,2,3,3]
输出:7, nums = [0,0,1,1,2,3,3]
解释:函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104-104 <= nums[i] <= 104nums已按升序排列
双指针法(快慢指针)
解题思路
- 初始化
low和fast指针为2。因为此问题允许每个元素最多重复两次,所以前两个元素我们不需要检查,直接保留即可。 - 使用一个
while循环处理fast指向的元素- 如果当前
fast指针指向的元素与low指向的元素的前两个元素不相等 (nums[low - 2] !== nums[fast]), 那么这个元素是需要保留的,我们就把这个元素复制到low指针的位置,然后low指针向前移动一位,fast指针也向前移动一位 - 如果
nums[low - 2]和nums[fast]相等,这意味着有重复超过两次的元素存在,因此我们只将fast指针向后移动一位
- 如果当前
- 循环结束后,数组中
low索引之前的元素就是处理后的结果,返回low作为新长度。
需要注意的是,这个函数会直接更改原数组,而非创建一个新的数组。此函数的空间复杂度为 O(1),即使用了常数量级的额外空间。
// 定义名为removeDuplicates的函数,用于移除排序数组中的重复元素,每个元素最多保留两个
var removeDuplicates = function (nums) {
// 获取数组长度
const len = nums.length;
// 如果数组长度小于等于2,无需移除重复元素,直接返回数组长度
if (len <= 2) {
return len;
}
// 初始化两个指针,分别表示当前元素的位置(low)和遍历数组的位置(fast)
let low = 2, fast = 2;
// 遍历数组
while (fast < len) {
// 检查当前元素和前两个元素是否相同,如果不同,则将当前元素放置在low的位置,并移动low指针
if (nums[low - 2] !== nums[fast]) {
nums[low] = nums[fast];
low++;
}
// 移动fast指针,继续遍历数组
fast++;
}
// 返回新数组的长度,即保留重复元素最多两次后的数组长度
return low;
};
罗马数字转整数(简)
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。
示例 1:
输入: s = "III"
输出: 3
示例 2:
输入: s = "IV"
输出: 4
示例 3:
输入: s = "IX"
输出: 9
示例 4:
输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
1 <= s.length <= 15s仅含字符('I', 'V', 'X', 'L', 'C', 'D', 'M')- 题目数据保证
s是一个有效的罗马数字,且表示整数在范围[1, 3999]内 - 题目所给测试用例皆符合罗马数字书写规则,不会出现跨位等情况。
- IL 和 IM 这样的例子并不符合题目要求,49 应该写作 XLIX,999 应该写作 CMXCIX 。
- 关于罗马数字的详尽书写规则,可以参考 罗马数字 - Mathematics 。
解题思路
“当前位置的元素比下个位置的元素小,就减去当前值,否则加上当前值”。
例如 XIV 可视作X-I+V=10-1+5=14
var romanToInt = function(s) {
const symbolValues = new Map();
symbolValues.set('I', 1);
symbolValues.set('V', 5);
symbolValues.set('X', 10);
symbolValues.set('L', 50);
symbolValues.set('C', 100);
symbolValues.set('D', 500);
symbolValues.set('M', 1000);
let ans = 0;
const n = s.length;
for (let i = 0; i < n; ++i) {
const value = symbolValues.get(s[i]);
if (i < n - 1 && value < symbolValues.get(s[i + 1])) {
ans -= value;
} else {
ans += value;
}
}
return ans;
};
最长公共前缀(简)
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。
提示:
1 <= strs.length <= 2000 <= strs[i].length <= 200strs[i]仅由小写英文字母组成
提示
- 假设第一个字符串为初始的最长公共前缀
- 循环直到所有字符串都以当前的前缀开头
- 如果不是所有字符串都以当前前缀开头,则缩短前缀长度
var longestCommonPrefix = function (strs) {
let str = strs[0]
while (!strs.every(item => item.startsWith(str))) {
str = str.slice(0, str.length - 1)
}
return str ?? ""
};
子集(中)
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示
- 1 <= nums.length <= 10
- -10 <= nums[i] <= 10
- nums 中的所有元素 互不相同
解题思路
- 迭代法:
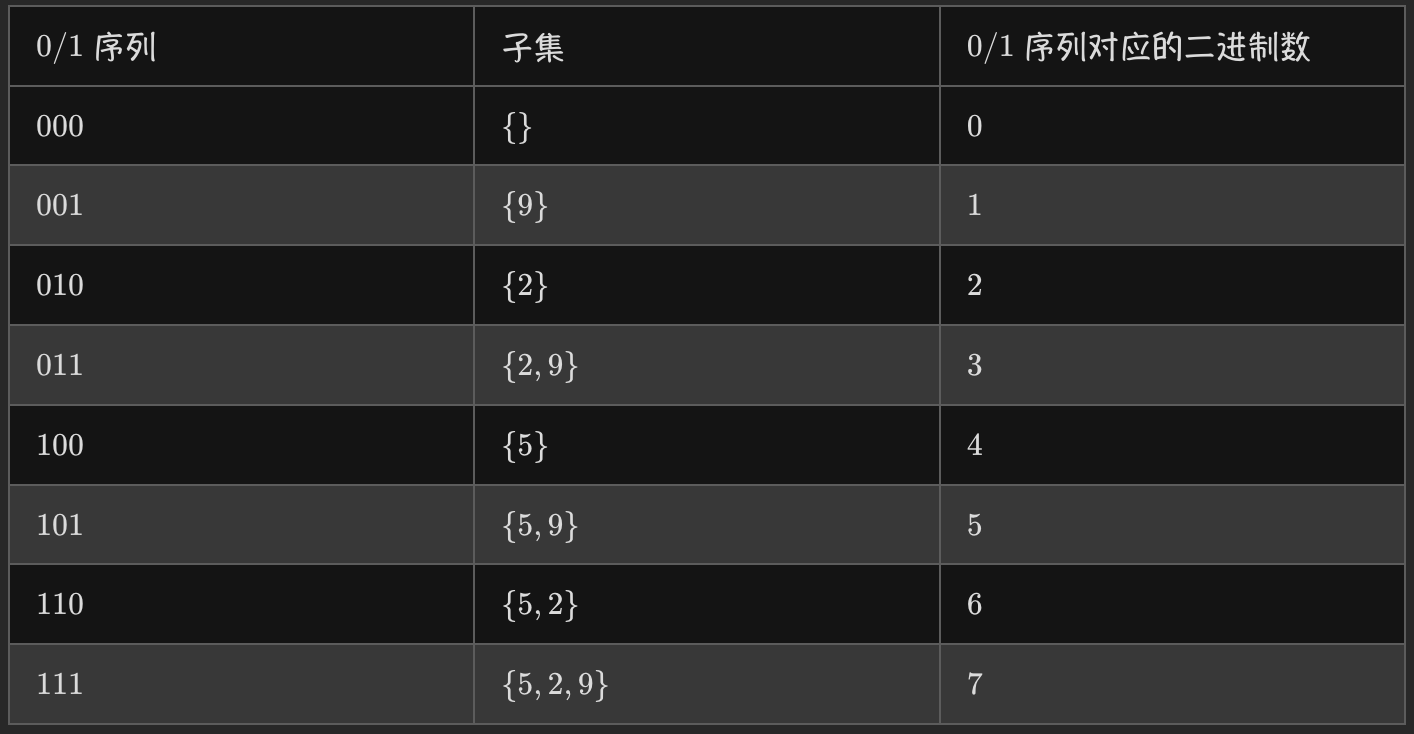
- 回溯法
迭代法
var subsets = function(nums) {
const ans = [];
const n = nums.length;
for (let mask = 0; mask < (1 << n); ++mask) {
const t = [];
// 在mask对应的二进制数中检查第i位是否为1。 如果是1,则将nums[i]加入t。
for (let i = 0; i < n; ++i) {
if (mask & (1 << i)) {
t.push(nums[i]);
}
}
ans.push(t);
}
return ans;
};
回溯法
var subsets = function(nums) {
const t = [];
const ans = [];
const dfs = (cur) => {
if (cur === nums.length) {
ans.push(t.slice());
return;
}
t.push(nums[cur]);
dfs(cur + 1);
t.pop(t.length - 1);
dfs(cur + 1);
}
dfs(0);
return ans;
};
盛最多水的容器(中)
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示
- n == height.length
- 2 <= n <= 105
- 0 <= height[i] <= 104
解题思路
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽底边宽度变短:
若向内 移动短板,水槽的短板可能变大,因此下个水槽的面积可能增大。
若向内移动长板,水槽的短板不变或变小,因比下个水槽的面积一定变小。
因此,初始化双指针分列水槽左右两端,循环每轮将短板向内移动一格,并更新面积最大值,直到两指针相遇时跳出;即可获得最大面积。
var maxArea = function (height) {
let i = 0;
let j = height.length - 1;
let res = 0;
while (j > i) {
res = Math.max(res, Math.min(height[i], height[j]) * (j - i));
height[i] > height[j] ? j-- : i++;
}
return res;
};
def maxArea(height):
i = 0
j = len(height) - 1
res = 0
while j > i:
res = max(res, min(height[i], height[j]) * (j - i))
j -= height[i] > height[j]
i += height[i] <= height[j]
return res
public static int maxArea(int[] height) {
int i = 0;
int j = height.length - 1;
int res = 0;
while (j > i) {
res = Math.max(res, Math.min(height[i], height[j]) * (j - i));
j -= height[i] > height[j] ? 1 : 0;
i += height[i] <= height[j] ? 1 : 0;
}
return res;
}
#include <algorithm>
#include <vector>
using namespace std;
class Solution {
public:
int maxArea(vector<int>& height) {
int i = 0;
int j = height.size() - 1;
int res = 0;
while (j > i) {
res = max(res, min(height[i], height[j]) * (j - i));
j -= height[i] > height[j] ? 1 : 0;
i += height[i] <= height[j] ? 1 : 0;
}
return res;
}
};
蜗牛排序(中)
请你编写一段代码为所有数组实现 snail(rowsCount,colsCount) 方法,该方法将 1D 数组转换为以蜗牛排序的模式的 2D 数组。无效的输入值应该输出一个空数组。当 rowsCount * colsCount !==nums.length 时。这个输入被认为是无效的。
蜗牛排序从左上角的单元格开始,从当前数组的第一个值开始。然后,它从上到下遍历第一列,接着移动到右边的下一列,并从下到上遍历它。将这种模式持续下去,每列交替变换遍历方向,直到覆盖整个数组。例如,当给定输入数组 [19, 10, 3, 7, 9, 8, 5, 2, 1, 17, 16, 14, 12, 18, 6, 13, 11, 20, 4, 15] ,当 rowsCount = 5 且 colsCount = 4 时,需要输出矩阵如下图所示。注意,矩阵沿箭头方向对应于原数组中数字的顺序
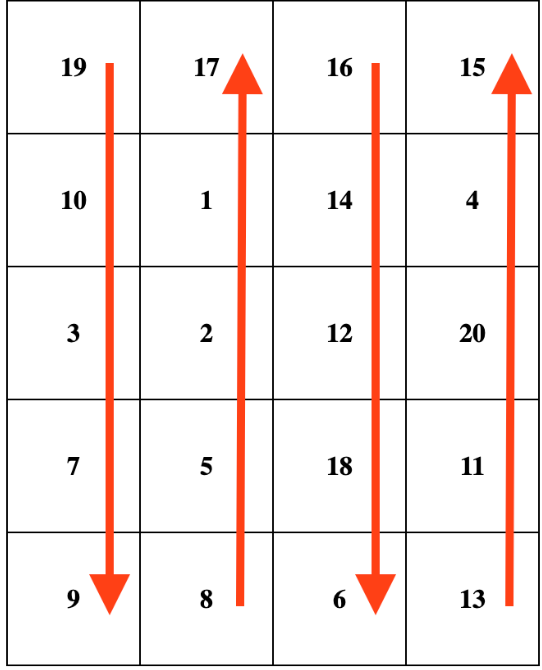
示例 1:
输入:
nums = [19, 10, 3, 7, 9, 8, 5, 2, 1, 17, 16, 14, 12, 18, 6, 13, 11, 20, 4, 15]
rowsCount = 5
colsCount = 4
输出:
[
[19,17,16,15],
[10,1,14,4],
[3,2,12,20],
[7,5,18,11],
[9,8,6,13]
]
示例 2:
输入:
nums = [1,2,3,4]
rowsCount = 1
colsCount = 4
输出:[[1, 2, 3, 4]]
示例 3:
输入:
nums = [1,3]
rowsCount = 2
colsCount = 2
输出:[]
Explanation: 2 * 2 = 4, 且原数组 [1,3] 的长度为 2; 所以,输入是无效的。
提示
- 0 <= nums.length <= 250
- 1 <= nums[i] <= 1000
- 1 <= rowsCount <= 250
- 1 <= colsCount <= 250
解题思路
有两种:
利用数组的转置
- 将数组按照行数分割
- 然后将偶数行的数组进行翻转
- 将翻转后的函数进行转置即为最终的结果
一层for循环
使用一个布尔变量 seq 来记录当前遍历的方向,true 代表正向,false 代表逆向。使用变量 start 来记录当前要填充的行数或列数。在遍历一维数组时,先将元素插入到当前的行或列中,然后根据 seq 值来判断方向。如果当前为正向,则向下移动一行或向右移动一列;若为逆向,则向上移动一行或向左移动一列。
/**
* @param {number} rowsCount
* @param {number} colsCount
* @return {Array<Array<number>>}
*/
function transposeArray(array) {
return array[0].map((_, colIndex) => array.map((row) => row[colIndex]))
}
function reverseEven(array) {
return array.map((row, rowIndex) => {
if (rowIndex % 2 === 0) {
return row
}
return row.reverse()
})
}
Array.prototype.snail = function (rowsCount, colsCount) {
if (rowsCount * colsCount !== this.length) return []
const res = []
let copy = JSON.parse(JSON.stringify(this))
while (copy.length >= rowsCount) {
res.push(copy.splice(0, rowsCount))
}
return transposeArray(reverseEven(res))
}
/**
* const arr = [1,2,3,4];
* arr.snail(1,4); // [[1,2,3,4]]
*/
/**
* @param {number} rowsCount
* @param {number} colsCount
* @return {Array<Array<number>>}
*/
Array.prototype.snail = function(rowsCount, colsCount) {
if (this.length !== rowsCount * colsCount) {
return [];
}
const res = [];
for (let i = 0; i < rowsCount; i++) {
res.push([]);
}
let seq = true; // 正向还是逆向
let start = 0;
for (let i = 0; i < this.length; i++) {
res[start].push(this[i]);
if (seq) {
if (start === rowsCount - 1) {
seq = false;
} else {
start++;
}
} else {
if (start === 0) {
seq = true;
} else {
start--;
}
}
}
return res;
}
合并区间(中)
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示
- 1 <= intervals.length <= 104
- intervals[i].length == 2
- 0 <= starti <= endi <= 104
解题思路
- 通过根据区间的起始时间进行排序
- 然后依次比较每个区间与前一个区间。
- 如果当前区间的开始时间在前一个区间的结束时间之后,代表它们不重叠,可以将前一个区间添加到结果数组中。
- 如果它们重叠,前一个区间的结束时间将延长到其自身结束时间和当前区间结束时间的最大值。
- 最后将最后一个区间添加到结果数组中。
var merge = function (intervals) {
intervals.sort((a, b) => a[0] - b[0]);
let prev = intervals[0]
let result = []
for (let i = 1; i < intervals.length; i++) {
let cur = intervals[i]
if (cur[0] > prev[1]) {
result.push(prev)
prev = cur
} else {
prev[1] = Math.max(cur[1], prev[1])
}
}
result.push(prev)
return result
};
三数之和(中)
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示
- 3 <= nums.length <= 3000
- -105 <= nums[i] <= 105
排序 + 双指针
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function (nums) {
// 升序
nums.sort((a, b) => a - b);
// 双指针法
let res = [];
for (let i = 0; i < nums.length; i++) {
// 一组中第一个元素大于0 直接返回
if (nums[i] > 0) return res;
let left = i + 1;
let right = nums.length - 1;
// 去重,当起始的值等于前一个元素,那么得到的结果将会和前一次相同
if (nums[i] == nums[i - 1]) continue;
while (right > left) {
let sum = nums[i] + nums[left] + nums[right]
if (sum > 0) {
right--;
} else if (sum < 0) {
left++;
} else {
// 数组中添加数组
res.push([nums[i], nums[left], nums[right]]);
// 在将左指针和右指针移动的时候,先对左右指针的值,进行判断
// 如果重复,直接跳过。
// 去重,因为 i 不变,当此时 l取的数的值与前一个数相同,所以不用在计算,直接跳
while (right > left && nums[left] == nums[left + 1]) {
left++;
}
// 去重,因为 i 不变,当此时 r取的数的值与前一个数相同,所以不用在计算,直接跳
while (right > left && nums[right] == nums[right - 1]) {
right--;
}
// 将左指针右移,将右指针左移。
left++;
right--;
}
}
}
return res;
};
二进制字符串前缀一致的次数(中)
给你一个长度为 n 、下标从 1 开始的二进制字符串,所有位最开始都是 0 。我们会按步翻转该二进制字符串的所有位(即,将 0 变为 1)。
给你一个下标从 1 开始的整数数组 flips ,其中 flips[i] 表示对应下标 i 的位将会在第 i 步翻转。
二进制字符串 前缀一致 需满足:在第 i 步之后,在 闭 区间 [1, i] 内的所有位都是 1 ,而其他位都是 0 。
返回二进制字符串在翻转过程中 前缀一致 的次数。
示例 1:
输入:flips = [3,2,4,1,5]
输出:2
解释:二进制字符串最开始是 "00000" 。
执行第 1 步:字符串变为 "00100" ,不属于前缀一致的情况。
执行第 2 步:字符串变为 "01100" ,不属于前缀一致的情况。
执行第 3 步:字符串变为 "01110" ,不属于前缀一致的情况。
执行第 4 步:字符串变为 "11110" ,属于前缀一致的情况。
执行第 5 步:字符串变为 "11111" ,属于前缀一致的情况。
在翻转过程中,前缀一致的次数为 2 ,所以返回 2 。
示例 2:
输入:flips = [4,1,2,3]
输出:1
解释:二进制字符串最开始是 "0000" 。
执行第 1 步:字符串变为 "0001" ,不属于前缀一致的情况。
执行第 2 步:字符串变为 "1001" ,不属于前缀一致的情况。
执行第 3 步:字符串变为 "1101" ,不属于前缀一致的情况。
执行第 4 步:字符串变为 "1111" ,属于前缀一致的情况。
在翻转过程中,前缀一致的次数为 1 ,所以返回 1 。
提示:
n == flips.length1 <= n <= 5 * 104flips是范围[1, n]中所有整数构成的一个排列
解题思路
在第 i 次翻转之后,我们希望 [1,i] 内的所有位都是 1,这等价于「前 i 次翻转中下标的最大值等于 i」。
因此,我们对数组 flip 进行遍历,同时记录翻转下标的最大值。当遍历到位置 i 时,如果最大值恰好等于 i,那么答案加 1。
需要注意数组的下标是从 0 开始的,因此在实际的代码编写中,判断的值为 i - 1。
/**
* @param {number[]} flips
* @return {number}
*/
var numTimesAllBlue = function(flips) {
let res = 0;
let max = 0;
for(let i = 0;i < flips.length;i++) {
// 记录下标的最大值
max = Math.max(max,flips[i])
if(i === max - 1) {
res++
}
}
return res
};
跳跃游戏(中)
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
贪心算法
解题思路(找不能)
- 定义一个变量用来记录可以跳跃的最大距离。
- 遍历数组,一旦可以跳跃的最大距离小于当前的下标,那么就代表不能够到达最后一个下标,否则更新可以跳跃的最大距离。
- 如果遍历到最后一个元素,代表能够到达最后一个下标。
/**
* @param {number[]} nums
* @return {boolean}
*/
var canJump = function (nums) {
let cover = 0;
for (let i = 0; i < nums.length; i++) {
// 一旦可以跳跃的最大距离小于当前的下标,那么就代表不能够到达最后一个下标
if (cover < i) return false
// 更新可以跳跃的最大距离
cover = Math.max(cover, i + nums[i])
}
return true
};
解题思路(找能)
- 定义一个变量用来记录可以跳跃的最大距离,初始值为第一个元素的值。
- 遍历当前能跳跃的最大距离,如果可以跳跃的最大距离大于等于数组的长度,那么就代表能够到达最后一个下标。
- 如果遍历完,那么就代表没有找到能够到达最后一个下标的元素。
var canJump = function (nums) {
// 长度为1 直接就是终点
if (nums.length === 1) return true;
let cover = nums[0];
for (let i = 0; i <= cover; i++) {
cover = Math.max(cover, i + nums[i]);
if (cover >= nums.length - 1) return true
}
return false
};
解题思路(从后往前)
- 定义一个变量end,表示必须到达的位置,初始为最后一个下标。
- 从后往前遍历数组,对于每个位置i,如果end-i小于等于nums[i],说明从i可以跳到end,那么就更新end为i,表示只要能到达i,就能到达最后。
- 最后判断end是否为0,如果是,说明可以从第一个位置跳到最后一个位置,否则不行。
var canJump = function (nums) {
// 必须到达end下标的数字
let end = nums.length - 1;
for (let i = nums.length - 2; i >= 0; i--) {
if (end - i <= nums[i]) {
end = i;
}
}
return end == 0;
};
跳跃游戏II(中)
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
贪心算法
解题思路
- 初始化当前位置(
curIndex)和下一个位置(nextIndex)为0,步数(steps)为0。 - 遍历数组,对于每个位置,计算能够到达的下一个位置(
nextIndex)。 - 如果当前位置等于之前设定的当前位置(
curIndex),说明已经达到了当前步数的最远位置,更新当前位置为新的最远位置(nextIndex),步数加1。 - 重复步骤2和步骤3,直到遍历完整个数组。
- 返回步数作为结果。
var jump = function(nums) {
let curIndex = 0
let nextIndex = 0
let steps = 0
for(let i = 0; i < nums.length - 1; i++) {
nextIndex = Math.max(nums[i] + i, nextIndex)
if(i === curIndex) {
curIndex = nextIndex
steps++
}
}
return steps
};
H 指数(中)
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且每篇论文 至少 被引用 h 次。如果 h 有多种可能的值,h 指数 是其中最大的那个。
示例 1:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。
示例 2:
输入:citations = [1,3,1]
输出:1
排序
解题思路
h指数的定义要求有h篇论文分别被引用了至少h次,所以如果当前的元素值大于h,说明这篇论文满足条件,可以将h指数增加一。例如,如果排序后的数组是[6, 5, 3, 1, 0],那么当遍历到第一个元素6时,h=0,因为6>0,所以将h加一,变为1。当遍历到第二个元素5时,h=1,因为5>1,所以将h加一,变为2。当遍历到第三个元素3时,h=2,因为3>2,所以将h加一,变为3。当遍历到第四个元素1时,h=3,因为1<=3,所以无法增加h指数,终止遍历。最终的h指数是3。
反序
var hIndex = function (citations) {
citations.sort((a, b) => b - a);
let h = 0;
for (let i = 0; i < citations.length; i++) {
if (citations[i] > h) {
h++;
}
}
return h;
};
正序
var hIndex = function(citations) {
citations.sort((a, b) => a - b);
let h = 0, i = citations.length - 1;
while (i >= 0 && citations[i] > h) {
h++;
i--;
}
return h;
};
除自身以外数组的乘积(中)
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 **不要使用除法,**且在 O(*n*) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
**进阶:
你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
方法一:左右乘积列表
解题思路
我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
- 初始化两个空数组 L 和 R。对于给定索引 i,L[i] 代表的是 i 左侧所有数字的乘积,R[i] 代表的是 i 右侧所有数字的乘积。
- 我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L,L[0] 应该是 1,因为第一个元素的左边没有元素。对于其他元素:L[i] = L[i-1] * nums[i-1]。
- 同理,对于数组 R,R[length-1] 应为 1。length 指的是输入数组的大小。其他元素:R[i] = R[i+1] * nums[i+1]。
- 当 R 和 L 数组填充完成,我们只需要在输入数组上迭代,且索引 i 处的值为:L[i] * R[i]。
var productExceptSelf = function (nums) {
const len = nums.length;
const L = [];
const R = [];
const answer = [];
L[0] = 1;
for (let i = 1; i < len; i++) {
L[i] = nums[i - 1] * L[i - 1]
}
R[len - 1] = 1;
for (let i = len - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1]
}
for (let i = 0; i < len; i++) {
answer[i] = L[i] * R[i];
}
return answer
};
方法二:空间复杂度 O(1) 的方法
解题思路
尽管上面的方法已经能够很好的解决这个问题,但是空间复杂度并不为常数。
由于输出数组不算在空间复杂度内,那么我们可以将 L 或 R 数组用输出数组来计算。先把输出数组当作 L 数组来计算,然后再动态构造 R 数组得到结果。让我们来看看基于这个思想的算法。
- 初始化 answer 数组,对于给定索引 i,answer[i] 代表的是 i 左侧所有数字的乘积。
- 构造方式与之前相同,只是我们试图节省空间,先把 answer 作为方法一的 L 数组。
- 这种方法的唯一变化就是我们没有构造 R 数组。而是用一个遍历来跟踪右边元素的乘积。并更新数组 answer[i]=answer[i]∗R。然后 R 更新为 R=R∗nums[i],其中变量 R 表示的就是索引右侧数字的乘积。
var productExceptSelf = function(nums) {
const length = nums.length;
const answer = [];
// answer[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素, 所以 answer[0] = 1
answer[0] = 1;
for (let i = 1; i < length; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
// R 为右侧所有元素的乘积
// 刚开始右边没有元素,所以 R = 1
let R = 1;
for (let i = length - 1; i >= 0; i--) {
// 对于索引 i,左边的乘积为 answer[i],右边的乘积为 R
answer[i] = answer[i] * R;
// R 需要包含右边所有的乘积,所以计算下一个结果时需要将当前值乘到 R 上
R *= nums[i];
}
return answer;
};
加油站(中)
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
一次遍历
解题思路
双层循环:
- 外循环遍历每一个加油站
- 初始化当前起始加油站的汽油总量和消耗总量
- 记录成功走过的加油站数量
- 如果成功走过所有加油站,返回起始加油站索引
- 否则,更新起始加油站索引,继续尝试
- 内循环在当前起始加油站开始尝试走完一圈
- 计算当前加油站的索引
- 累加汽油量和消耗量
- 如果消耗超过汽油量,无法到达下一站,退出内层循环
- 成功走过一个加油站,增加计数
无法完成一圈,结束程序,返回-1
var canCompleteCircuit = function(gas, cost) {
// 获取加油站数量
const n = gas.length;
// 初始化起始加油站索引
let i = 0;
// 遍历加油站数组
while (i < n) {
// 初始化当前起始加油站的汽油总量和消耗总量
let sumOfGas = 0, sumOfCost = 0;
// 记录成功走过的加油站数量
let cnt = 0;
// 在当前起始加油站开始尝试走完一圈
while (cnt < n) {
// 计算当前加油站的索引
const j = (i + cnt) % n;
// 累加汽油量和消耗量
sumOfGas += gas[j];
sumOfCost += cost[j];
// 如果消耗超过汽油量,无法到达下一站,退出内层循环
if (sumOfCost > sumOfGas) {
break;
}
// 成功走过一个加油站,增加计数
cnt++;
}
// 如果成功走过所有加油站,返回起始加油站索引
if (cnt === n) {
return i;
} else {
// 否则,更新起始加油站索引,继续尝试
i = i + cnt + 1;
}
}
// 无法完成一圈,返回-1
return -1;
};
解题思路
首先我们有两个结论:
- 如果 left 累加 gas[i]−cost[i] 后,小于 0。则出发点到站 i 都不是起点。
- 如果总加油量 sum(gas)>=sum(cost)总耗油量,问题一定有解。
具体步骤:
- 遍历每个加油站
- 统计总汽油量和总汽油花费
- 更新当前剩余汽油,若剩余汽油为负值,表示无法到达下一站,更新起始加油站索引
- 若总汽油量小于总汽油花费,说明无法完成一圈旅行,结束程序,返回 -1
- 返回起始加油站索引
var canCompleteCircuit = function (gas, cost) {
// 初始化变量
let left = 0, // 当前剩余汽油
start = 0, // 起始加油站索引
totalGas = 0, // 总汽油量
totalCost = 0; // 总汽油花费
// 遍历每个加油站
for (let i = 0; i < gas.length; i++) {
// 统计总汽油量和总汽油花费
totalGas += gas[i];
totalCost += cost[i];
// 更新当前剩余汽油
left += gas[i] - cost[i];
// 若剩余汽油为负值,表示无法到达下一站,更新起始加油站索引
if (left < 0) {
start = i + 1;
left = 0;
}
}
// 若总汽油量小于总汽油花费,说明无法完成一圈旅行
if (totalGas < totalCost) {
return -1;
}
// 返回起始加油站索引
return start;
};
整数转罗马数字(中)
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给你一个整数,将其转为罗马数字。
示例 1:
输入: num = 3
输出: "III"
示例 2:
输入: num = 4
输出: "IV"
示例 3:
输入: num = 9
输出: "IX"
示例 4:
输入: num = 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.
示例 5:
输入: num = 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
1 <= num <= 3999
解题思路
根据罗马数字的唯一表示法,为了表示一个给定的整数 num,我们寻找不超过 num 的最大符号值,将 num 减去该符号值,然后继续寻找不超过 num 的最大符号值,将该符号拼接在上一个找到的符号之后,循环直至 num 为 0。最后得到的字符串即为 numm 的罗马数字表示。
编程时,可以建立一个数值-符号对的列表 valueSymbols,按数值从大到小排列。遍历valueSymbols 中的每个数值-符号对,若当前数值 value 不超过 num,则从 num 中不断减去 value 直至 num 小于 value,然后遍历下一个数值-符号对。若遍历中 numn 为 0 则跳出循环。
/**
* @param {number} num
* @return {string}
*/
var intToRoman = function (num) {
const valueSymbols = [[1000, "M"], [900, "CM"], [500, "D"], [400, "CD"], [100, "C"], [90, "XC"], [50, "L"], [40, "XL"], [10, "X"], [9, "IX"], [5, "V"], [4, "IV"], [1, "I"]];
const res = [];
for (let [val, key] of valueSymbols) {
while (num >= val) {
num -= val;
res.push(key)
}
if (num === 0) break
}
return res.join("")
};
分发糖果(难)
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
两次遍历
解题思路
- 第一次遍历:保证后面的孩子如果评分高于前面的孩子,就多得到一个糖果。这样可以满足从左往右看的条件。
- 第二次遍历:第一次遍历可能会导致一些孩子得到的糖果超过了最小的需要。所以,第二次遍历的时候,要用Math.max函数来比较当前孩子得到的糖果和他应该得到的糖果,取较大的那个。
var candy = function (ratings) {
// 条件判断
if (ratings.length < 1) {
return 0
}
// 至少每个人都有1个糖果
let result = new Array(ratings.length).fill(1);
// 正序,如果递增,后面在原来的基础上+1
for (let i = 0; i < ratings.length - 1; i++) {
if (ratings[i + 1] > ratings[i]) {
result[i + 1] = result[i] + 1
}
}
// 倒序,如果递增,与原来的值比较取最大值
for (let i = ratings.length - 1; i > 0; i--) {
if (ratings[i - 1] > ratings[i]) {
result[i - 1] = Math.max(result[i - 1], result[i] + 1);
}
}
// 返回总糖果数
return result.reduce((prev, cur) => prev += cur);
};
接雨水(难)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
方法一:按列求
解题思路
求每一列的水,我们只需要关注当前列,以及左边最高的墙,右边最高的墙就够了。
装水的多少,当然根据木桶效应,我们只需要看左边最高的墙和右边最高的墙中较矮的一个就够了。
具体算法:
遍历数组,找出当前列左边最高和右边最高,然后比较两者较小的一列与当前列的高度做比较:只有比当前列的高度高才能接水,接水量为:min - height[i]
var trap = function (height) {
let sum = 0;
for (let i = 0; i < height.length - 1; i++) {
// 找出左边最高
let max_left = 0;
for (let j = i - 1; j >= 0; j--) {
if (height[j] > max_left) {
max_left = height[j]
}
}
// 找出右边最高
let max_right = 0;
for (let j = i + 1; j < height.length; j++) {
if (height[j] > max_right) {
max_right = height[j]
}
}
// 找出两端较小的
let min = Math.min(max_left, max_right)
//只有较小的一段大于当前列的高度才会有水,其他情况不会有水
if (min > height[i]) {
sum += (min - height[i])
}
}
return sum
};
方法二:动态规划
解题思路
我们注意到,解法二中。对于每一列,我们求它左边最高的墙和右边最高的墙,都是重新遍历一遍所有高度,这里我们可以优化一下。
首先用两个数组,max_left [i] 代表第 i 列左边最高的墙的高度,max_right[i] 代表第 i 列右边最高的墙的高度。(一定要注意下,第 i 列左(右)边最高的墙,是不包括自身的,和 leetcode 上边的讲的有些不同)
对于 max_left我们其实可以这样求。
max_left [i] = Max(max_left [i-1],height[i-1])。它前边的墙的左边的最高高度和它前边的墙的高度选一个较大的,就是当前列左边最高的墙了。
对于 max_right我们可以这样求。
max_right[i] = Max(max_right[i+1],height[i+1]) 。它后边的墙的右边的最高高度和它后边的墙的高度选一个较大的,就是当前列右边最高的墙了。
这样,我们再利用解法二的算法,就不用在 for 循环里每次重新遍历一次求 max_left 和 max_right 了。
var trap = function (height) {
const n = height.length;
if (n <= 2) {
return 0; // 无法形成凹槽,直接返回0
}
let leftMax = new Array(n).fill(0);
let rightMax = new Array(n).fill(0);
// 预先计算每个位置左边的最高值
leftMax[0] = height[0];
for (let i = 1; i < n; i++) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
// 预先计算每个位置右边的最高值
rightMax[n - 1] = height[n - 1];
for (let i = n - 2; i >= 0; i--) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
let totalWater = 0;
// 计算每个位置上的水量
for (let i = 1; i < n - 1; i++) {
const minHeight = Math.min(leftMax[i - 1], rightMax[i + 1]);
if (minHeight > height[i]) {
totalWater += minHeight - height[i];
}
}
return totalWater;
};
方法三:双指针
解题思路
动态规划中,我们常常可以对空间复杂度进行进一步的优化。
在本题中,从两端向中间遍历数组,维护两个变量max_left和max_right,分别表示左右两端的最大高度。对于每个位置i,如果max_left > height[i],那么就可以在i处存储max_left - height[i]的雨水,同理,如果max_right > height[i],那么就可以在i处存储max_right - height[i]的雨水。
具体步骤:
首先,定义一个变量n,表示数组的长度。如果n小于等于2,那么直接返回0,因为无法形成凹槽。
然后,定义一个变量sum,表示总的雨水量,初始为0。
定义两个变量max_left和max_right,表示左右两端的最大高度,初始为0。
定义两个指针left和right,表示当前遍历的位置,初始为1和n-2,分别从左右两端开始。
使用一个for循环,从1到n-2遍历数组,计算每个位置上的雨水量。
如果height[left - 1] < height[right + 1],说明左边的柱子比右边的柱子低,那么就从左到右遍历。
- 更新max_left为max_left和height[left - 1]中的较大值,表示左边的最大高度。
- 如果max_left > height[left],说明当前位置可以存储雨水,那么就把max_left - height[left]加到sum上,表示当前位置的雨水量。
- 把left加1,表示向右移动一位。
否则,说明右边的柱子比左边的柱子低,那么就从右到左遍历。
- 更新max_right为max_right和height[right + 1]中的较大值,表示右边的最大高度。
- 如果max_right > height[right],说明当前位置可以存储雨水,那么就把max_right - height[right]加到sum上,表示当前位置的雨水量。
- 把right减1,表示向左移动一位。
最后,返回sum,表示数组中能够存储的雨水的总量
为什么height[left - 1] 小于 height[right + 1],就能说明左边的柱子比右边的柱子低?
- 假设height是一个长度为n的数组,表示n个柱子的高度,其中n > 2。
- 假设left和right是两个指针,表示当前遍历的位置,其中1 <= left < right <= n - 2。
- 假设max_left和max_right是两个变量,表示左右两端的最大高度,其中max_left = max(height[0], …, height[left - 1]),max_right = max(height[right + 1], …, height[n - 1])。
- 那么,如果height[left - 1] < height[right + 1],就能说明左边的柱子比右边的柱子低,即max_left < max_right,这是因为:
- 根据max_left的定义,我们有max_left <= height[left - 1]。
- 根据max_right的定义,我们有max_right >= height[right + 1]。
- 根据height[left - 1] < height[right + 1],我们有height[left - 1] < max_right。
- 综合上述三个不等式,我们有max_left < max_right,即左边的柱子比右边的柱子低
var trap = function (height) {
const n = height.length;
if (n <= 2) {
return 0; // 无法形成凹槽,直接返回0
}
let sum = 0;
let max_left = 0
let max_right = 0;
let left = 1;
let right = n - 2
// 计算每个位置上的水量
for (let i = 1; i < n - 1; i++) {
// 从左到右
if(height[left - 1] < height[right + 1]) {
max_left = Math.max(max_left,height[left - 1]);
if(max_left > height[left]) {
sum += (max_left - height[left])
}
left++
// 从左到右
} else {
max_right =Math.max(max_right,height[right + 1]);
if(max_right > height[right]) {
sum += (max_right - height[right])
}
right--;
}
}
return sum;
};