案例

GodX...大约 23 分钟

反转链表(简)

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
示例 2：

输入：head = [1,2]
输出：[2,1]
示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

解题

迭代

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function(head) {
    // 生成新的头节点
    let prev = null;
    // 将指针指向头节点
    let curr = head;
    while (curr) {
        // 用一个临时变量将当前节点的下一个节点保存起来
        const next = curr.next;
        // 将指针指向前一个节点
        curr.next = prev;
        // 为下一次遍历做准备，将前一个节点向前移动
        prev = curr;
        // 为下一次遍历做准备，当前节点向前移动
        curr = next;
    }
    return prev;
};

递归

大问题拆解成两个子问题
子问题求解方式和大问题一样
存在最小子问题（递归边界）

var reverseList = function(head) {
 		// 递归终止条件：空链表或者只存在一个节点
    if (head == null || head.next == null) return head
  	// 递归调用子问题
    const p = reverseList(head.next)
    // 反转
    head.next.next = head
    head.next = null
    return p
};

环形链表(简)

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。

**进阶：**你能用 O(1)（即，常量）内存解决此问题吗？

解题思路

利用 JSON.stringfy()的检测机制
这个算法利用了JSON.stringify方法的一个特性来检测链表中是否存在环。JSON.stringify方法在尝试序列化一个对象时，如果对象中存在循环引用（即对象直接或间接地引用了自身），会抛出一个TypeError异常。在链表中，如果存在环，那么在序列化链表时就会遇到循环引用的情况，因此JSON.stringify会抛出异常。
这个方法的代码逻辑是：
1. 尝试使用JSON.stringify序列化链表。
2. 如果在序列化过程中没有抛出异常，说明链表中没有环，函数返回false。
3. 如果抛出了TypeError异常，说明在序列化过程中遇到了循环引用，即链表中存在环，函数返回true。
这种方法是一种非传统的检测链表环的方式，它利用了JavaScript引擎内部对循环引用的处理机制。虽然这种方法可以工作，但它并不是检测链表环的标准方法，因为它依赖于JSON.stringify的异常机制，而且在性能上可能不如传统的快慢指针方法。此外，这种方法也不能提供环的其他信息，如环的起始节点或环的长度。
标志位
给遍历过的节点打记号，如果遍历过程中遇到有记号的说明已环.
快慢指针
问：兔子会不会「跳过」乌龟，从来不会和乌龟相遇呢？
答：这是不可能的。如果有环的话，那么兔子和乌龟都会进入环中。这时用「相对速度」思考，乌龟不动，兔子相对乌龟每次只走一步，这样就可以看出兔子一定会和乌龟相遇了。

JSON.stringfy()

var hasCycle = function (head) {
    try {
        JSON.stringify(head)
    } catch{
        return true
    }
    return false
};

标志位

var hasCycle = function(head) {
    while(head) {
        if(head.tag) return true;
        head.tag = true;
        head = head.next;
    }
    return false
};

快慢指针

// 定义一个函数，用于检测链表是否有环
var hasCycle = function(head) {
    // 初始化慢指针和快指针都指向链表头节点
    let slow = head;
    let fast = head;
    // 当快指针和快指针的下一个节点都存在时，执行循环
    while(fast && fast.next) {
        // 慢指针每次移动一步
        slow = slow.next;
        // 快指针每次移动两步
        fast = fast.next.next;
        // 如果慢指针和快指针相遇，说明链表有环，返回true
        if(slow === fast) {
            return true
        }
    }
    // 如果循环结束仍未相遇，说明链表无环，返回false
    return false
};

两数相加(中)

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示

每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零

解题思路

将两个链表看成是相同长度的进行遍历，如果一个链表较短则在前面补
0，比如 987 + 23 = 987 + 023 = 1010
每一位计算的同时需要考虑上一位的进位问题，而当前位计算结束后同样需要更新进位值
如果两个链表全部遍历完毕后，进位值为 1,则在新链表最前方添加节点

var addTwoNumbers = function (l1, l2) {
  let head = null, // 头部
    tail = null; // 尾部
  let carry = 0; // 进位
  // 当 l1 或者 l2 没有遍历到尾部时
  while (l1 || l2) {
    // 没有值默认为 0
    const n1 = l1 ? l1.val : 0;
    const n2 = l2 ? l2.val : 0;
    // 当前位纵向相加（包括进位）
    const sum = n1 + n2 + carry;
    if (!head) {
      // 结果链表为空，代表为头部
      head = tail = new ListNode(sum % 10);
    } else {
      tail.next = new ListNode(sum % 10);
      tail = tail.next;
    }
    carry = Math.floor(sum / 10); // 更新进位值
    // 当前节点有值，将指针移动至下一个节点，为下次循环做准备
    if (l1) {
      l1 = l1.next;
    }
    if (l2) {
      l2 = l2.next;
    }
  }
  // 如果进位大于0,尾部新增一个节点
  if (carry > 0) {
    tail.next = new ListNode(carry);
  }
  // 返回链表
  return head;
};

合并两个有序链表(简)

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

解题思路

递归
迭代
我们可以用迭代的方法来实现上述算法。当 l1 和 l2 都不是空链表时，判断 l1 和 l2 哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。

递归

var mergeTwoLists = function (l1, l2) {
    if (l1 === null) {
        return l2;
    } else if (l2 === null) {
        return l1;
    } else if (l1.val < l2.val) {
        l1.next = mergeTwoLists(l1.next, l2);
        return l1;
    } else {
        l2.next = mergeTwoLists(l1, l2.next);
        return l2;
    }
};

迭代

var mergeTwoLists = function (list1, list2) {
    let dummy = new ListNode(); // 用哨兵节点简化代码逻辑
    let cur = dummy; // cur 指向新链表的末尾
    while (list1 && list2) {
        if (list1.val < list2.val) {
            cur.next = list1; // 把 list1 加到新链表中
            list1 = list1.next;
        } else { // 注：相等的情况加哪个节点都是可以的
            cur.next = list2; // 把 list2 加到新链表中
            list2 = list2.next;
        }
        cur = cur.next;
    }
    cur.next = list1 ? list1 : list2; // 拼接剩余链表
    return dummy.next;
};

随机链表的复制(中)

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。深拷贝应该正好由 n 个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

示例 1：

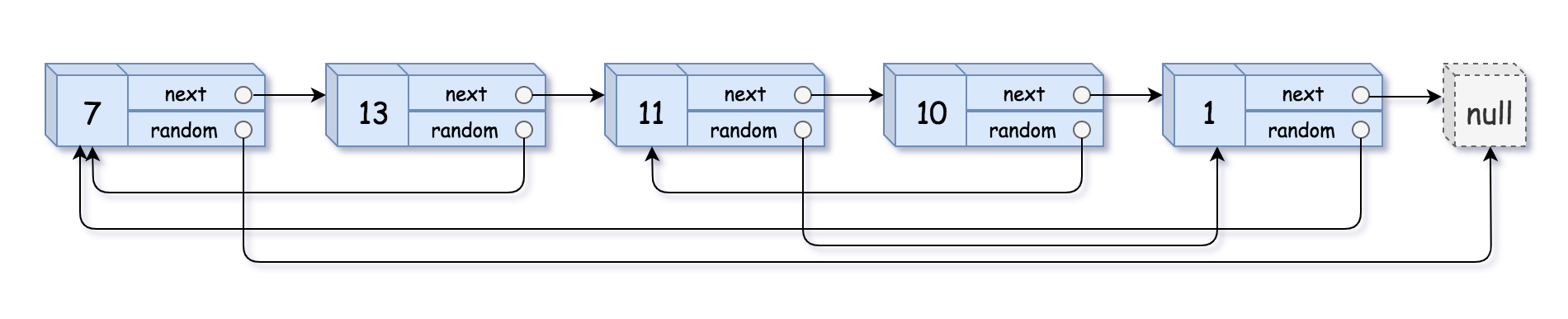
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

提示：

0 <= n <= 1000
-104 <= Node.val <= 104
Node.random 为 null 或指向链表中的节点。

解题思路

首先检查传入的头节点 head 是否为 null，如果是，则返回 null。
然后创建一个新的 Map 对象来存储原始节点和新创建的节点之间的映射关系。
使用一个循环，遍历原始链表，对于每个节点，都在 Map 中创建一个新的节点，并将原始节点作为键，新节点作为值存储起来。
再次遍历原始链表，这次是为了更新新节点的 next 和 random 指针。通过从 Map 中获取当前节点对应的新节点，然后分别设置其 next 和 random 指针指向 Map 中相应的节点。
最后，函数返回新链表的头节点，即 map.get(head)。

// 这个函数用于深拷贝一个特殊的链表，其中每个节点包含一个额外的随机指针
function copyRandomList(head) {
  // 如果头节点为空，则直接返回 null
  if (!head) return null;
  
  // 初始化当前节点为头节点
  let cur = head;
  // 创建一个新的 Map 对象来存储原节点和新节点之间的映射关系
  const map = new Map();
  
  // 第一次遍历，复制所有节点并创建原节点到新节点的映射
  while (cur) {
    map.set(cur, { val: cur.val }); // 创建新节点并加入到 Map 中
    cur = cur.next; // 移动到下一个节点
  }
  
  // 将 cur 重置为头节点，准备第二次遍历
  cur = head;
  
  // 第二次遍历，设置新节点的 next 和 random 指针
  while (cur) {
    // 设置新节点的 next 指针
    map.get(cur).next = map.get(cur.next) || null;
    // 设置新节点的 random 指针
    map.get(cur).random = map.get(cur.random) || null;
    // 移动到下一个节点
    cur = cur.next;
  }
  
  // 返回新链表的头节点
  return map.get(head);
}

反转链表 II(中)

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

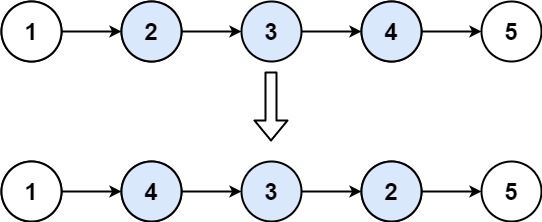
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

示例 2：

输入：head = [5], left = 1, right = 1
输出：[5]

提示：

链表中节点数目为 n
1 <= n <= 500
-500 <= Node.val <= 500
1 <= left <= right <= n

进阶： 你可以使用一趟扫描完成反转吗？

解题思路

我们以下图中黄色区域的链表反转为例。

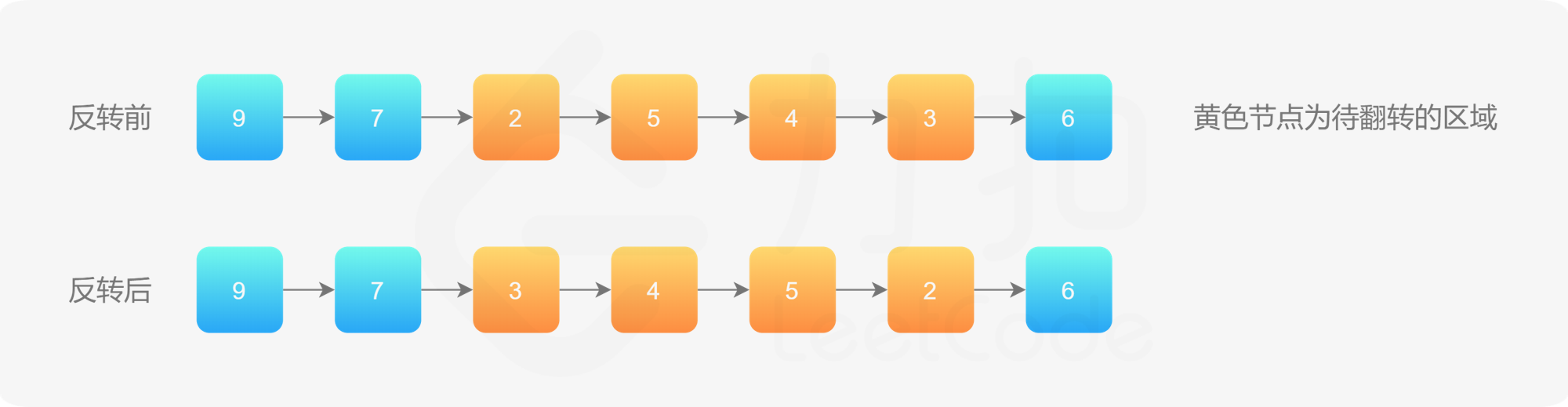
使用「206.反转链表」的解法，反转 left 到 right 部分以后，再拼接起来。我们还需要记录 left 的前一个节点，和 right 的后一个节点。如图所示：

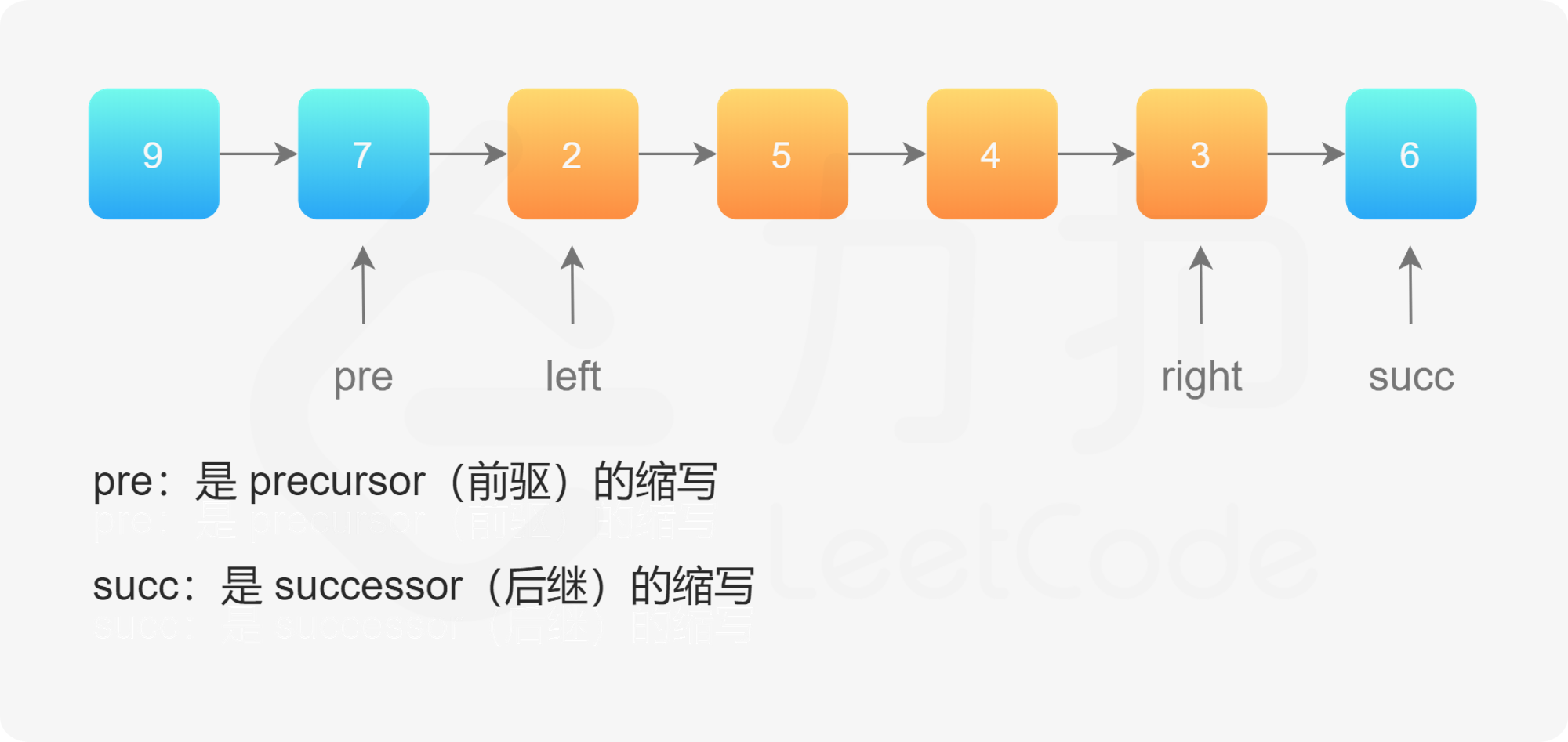
算法步骤

第1步：先将待反转的区域反转；
第2步：把 pre 的 next 指针指向反转以后的链表头节点，把反转以后的链表的尾节点的 next 指针指向 Succ 。

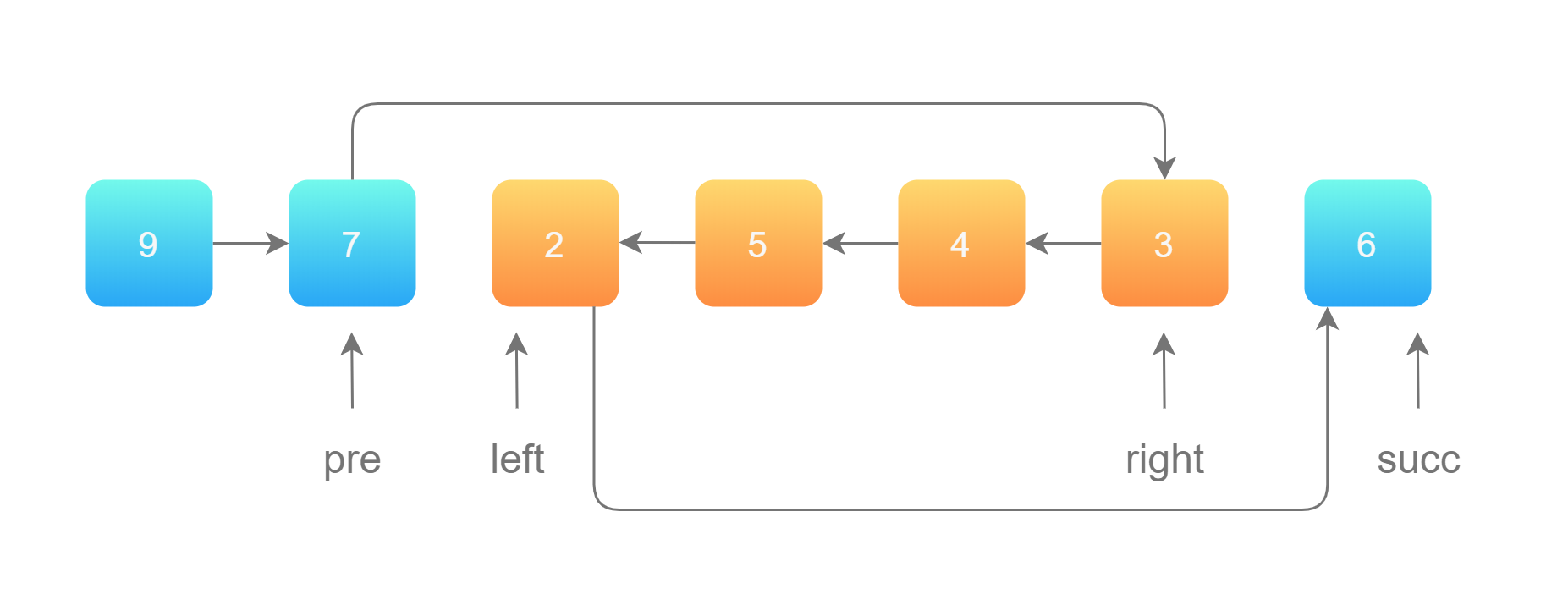
编码细节我们不在题解中介绍了，请见下方代码。思路想明白以后，编码不是一件很难的事情。这里要提醒大家的是，链接什么时候切断，什么时候补上去，先后顺序一定要想清楚，如果想不清楚，可以在纸上模拟，让思路清晰。

var reverseBetween = function(head, left, right) {
    // 因为头节点有可能发生变化，使用虚拟头节点可以避免复杂的分类讨论
    const dummyNode = new ListNode(-1);
    dummyNode.next = head;

    let pre = dummyNode;
    // 第 1 步：从虚拟头节点走 left - 1 步，来到 left 节点的前一个节点
    // 建议写在 for 循环里，语义清晰
    for (let i = 0; i < left - 1; i++) {
        pre = pre.next;
    }

    // 第 2 步：从 pre 再走 right - left + 1 步，来到 right 节点
    let rightNode = pre;
    for (let i = 0; i < right - left + 1; i++) {
        rightNode = rightNode.next;
    }

    // 第 3 步：切断出一个子链表（截取链表）
    let leftNode = pre.next;
    let curr = rightNode.next;

    // 注意：切断链接
    pre.next = null;
    rightNode.next = null;

    // 第 4 步：同第 206 题，反转链表的子区间
    reverseLinkedList(leftNode);

    // 第 5 步：接回到原来的链表中
    pre.next = rightNode;
    leftNode.next = curr;
    return dummyNode.next;
};

const reverseLinkedList = (head) => {
    let pre = null;
    let cur = head;

    while (cur) {
        const next = cur.next;
        cur.next = pre;
        pre = cur;
        cur = next;
    }
}

K 个一组翻转链表（难）

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

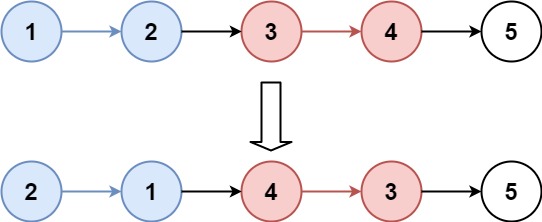
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

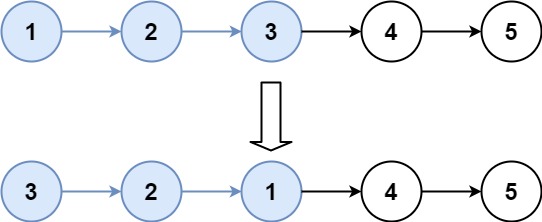
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

**进阶：**你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

解题思路

算法的思路是“K 个一组翻转链表”，其核心思想是分治和递归。以下是算法的主要步骤：

检查链表长度：首先检查链表是否有足够的 k 个节点。这通过遍历链表来完成，计数器从 1 开始，直到达到 k 或链表结束。
翻转节点：如果链表有足够的 k 个节点，则对这些节点进行翻转。翻转是通过改变节点指针的方向来实现的。这需要三个指针：当前节点（h）、前一个节点（pre）和下一个节点（t）。在每次迭代中，我们将当前节点的下一个节点指向前一个节点，然后更新这三个指针。
递归处理剩余部分：翻转完当前组的 k 个节点后，我们递归地对链表的剩余部分调用相同的函数。递归的结束条件是链表为空或链表长度小于 k。
连接翻转后的链表：递归调用返回的是剩余部分翻转后的新头节点。我们需要将这个新头节点连接到当前组翻转后的末尾。
返回结果：最后，返回翻转后的链表的头节点。

这个算法的关键在于递归和链表操作。它将大问题分解为小问题（每 k 个节点一组），然后递归地解决这些小问题。通过这种方式，算法能够有效地处理链表的翻转，同时保持代码的简洁和可读性。

function reverseKGroup(head, k) {
    if (!head) return null; // 如果链表为空，直接返回 null

    let p = head;
    let i = 1;
    // 检查链表是否有足够的 k 个节点
    while (p !== null && p.next !== null && i < k) {
        p = p.next;
        i++;
    }

    if (i < k) return head; // 如果不足 k 个节点，保持不变，返回 head

    let h = head;
    let pre = null;
    let next = p.next; // 保存下一组的起始节点
    // 翻转当前组的 k 个节点
    while (h !== next) {
        let t = h.next;
        h.next = pre;
        pre = h;
        h = t;
    }

    // 递归翻转下一组节点，并连接到当前组的末尾
    head.next = reverseKGroup(next, k);
    return p; // 返回当前组的新的头节点
}

删除链表的倒数第 N 个结点（中）

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

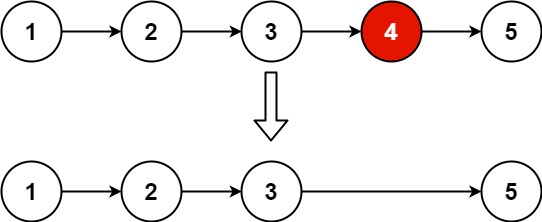
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

提示：

链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

进阶:你能尝试使用一趟扫描实现吗？

解题思路

两趟

首先调用reverse函数来反转链表。然后，它遍历反转后的链表，寻找要删除的节点。如果n是1，意味着要删除的是链表的最后一个节点，函数直接返回反转后的链表的下一个节点（即原链表的头节点）。如果找到了要删除的节点，就将该节点从链表中移除，然后再次反转链表，返回结果。

一趟

两趟算法的主要问题是效率。为了删除一个节点，它首先反转整个链表，然后删除节点，最后再次反转链表。这个过程的时间复杂度是O(N)，其中N是链表的长度。但实际上，我们不需要反转链表两次。我们可以通过一次遍历就找到要删除的节点。

一个更高效的算法是使用双指针技术。我们可以设置两个指针，第一个指针先向前移动n步，然后两个指针同时向前移动。当第一个指针到达链表的末尾时，第二个指针就位于要删除的节点之前。这样，我们就可以直接删除该节点，而不需要反转链表。

两趟

var removeNthFromEnd = function (head, n) {
    const temp = reverse(head);
    let index = 1;
    let curr = temp;
    while (curr) {
        if (n === 1) {
            return reverse(temp.next)
        } else if (index === n - 1) {
            curr.next = curr.next.next;
            return reverse(temp)
        }
        curr = curr.next;
        index++;
    }
};

var reverse = function (head) {
    let prev = null;
    let curr = head;
    while (curr) {
        const next = curr.next;
        curr.next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}

一趟

var removeNthFromEnd = function(head, n) {
    let dummy = new ListNode(0); // 创建一个哑节点，它的next指向head
    dummy.next = head;
    let first = dummy;
    let second = dummy;

    // 第一个指针向前移动n+1步
    for (let i = 0; i <= n; i++) {
        first = first.next;
    }

    // 当第一个指针到达链表的末尾时，第二个指针就位于要删除的节点之前
    while (first !== null) {
        first = first.next;
        second = second.next;
    }

    // 删除节点
    second.next = second.next.next;

    return dummy.next; // 返回哑节点的next，即新链表的头节点
};

删除排序链表中的重复元素 II（中）

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

示例 1：

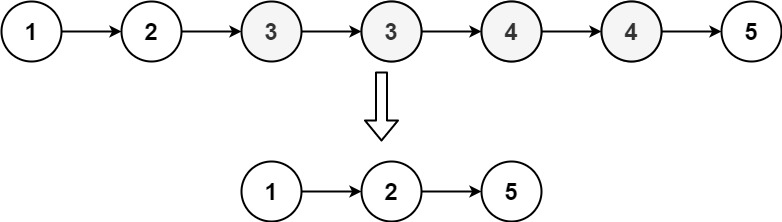
输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

示例 2：

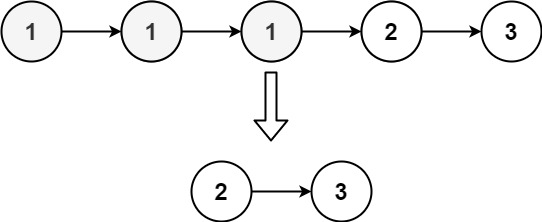
输入：head = [1,1,1,2,3]
输出：[2,3]

提示：

链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序排列

var deleteDuplicates = function (head) {
    let dummy = new ListNode(0); // 创建哑节点
    let tail = dummy; // tail 用于跟踪新链表的最后一个节点
    let curr = head;
    while (curr) {
        // 检查当前节点是否是重复节点
        if (curr.next && curr.val === curr.next.val) {
            // 跳过所有重复的节点
            while (curr.next && curr.val === curr.next.val) {
                curr = curr.next;
            }
        } else {
            // 如果当前节点不是重复节点，将其添加到新链表中
            tail.next = new ListNode(curr.val);
            tail = tail.next;
        }
        curr = curr.next;
    }
    return dummy.next; // 返回新链表的头节点
};

旋转链表（中）

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

示例 1：

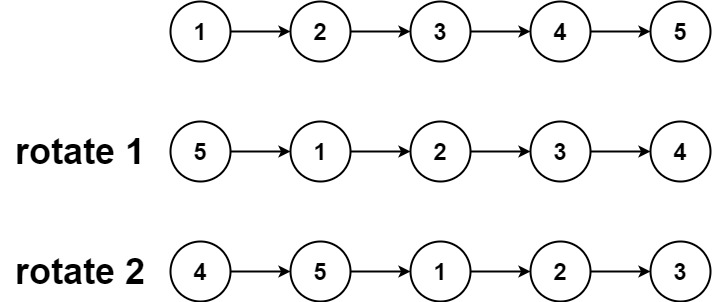
输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]

示例 2：

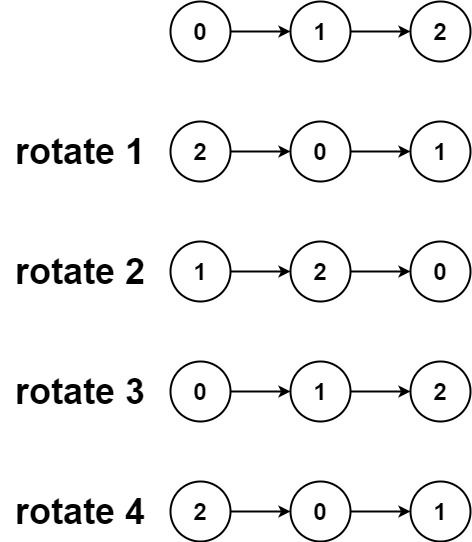
输入：head = [0,1,2], k = 4
输出：[2,0,1]

提示：

链表中节点的数目在范围 [0, 500] 内
-100 <= Node.val <= 100
0 <= k <= 2 * 109

解题思路

计算链表长度：首先，通过遍历链表，计算出链表的长度 n。这有助于后续确定旋转的位置。
处理特殊情况：如果旋转次数 k 为 0，或者链表为空或只有一个节点，则不需要旋转，直接返回头节点。
确定旋转位置：计算新的头节点位置 add，即 n - k % n。这里使用了取模运算，以处理 k 大于链表长度的情况。
形成循环链表：将链表的最后一个节点指向头节点，形成循环链表。这样做的目的是为了能够方便地找到旋转后的新头节点。
找到新的头节点：从链表的头节点开始，移动 add 次到达新的头节点的前一个位置。
断开链表并返回新头节点：将新的头节点的前一个节点的 next 指针设置为 null，断开循环链表，并返回新的头节点。

这个算法的关键在于通过形成循环链表来简化链表的旋转操作。通过这种方式，可以避免复杂的链表重组，只需简单地改变指针指向即可实现旋转。

var rotateRight = function(head, k) {
    // 如果旋转次数为0，或者链表为空或只有一个节点，直接返回头节点
    if (k === 0 || !head || !head.next) {
        return head;
    }

    let n = 1; // 记录链表的长度
    let cur = head; // 当前节点，用于遍历链表
    while (cur.next) {
        cur = cur.next;
        n++;
    }

    // 计算新的头节点位置
    let add = n - k % n;
    // 如果旋转次数是链表长度的倍数，则不需要旋转
    if (add === n) {
        return head;
    }

    // 将链表的最后一个节点指向头节点，形成循环链表
    cur.next = head;

    // 找到新的头节点的前一个节点
    while (add) {
        cur = cur.next;
        add--;
    }

    // 新的头节点是当前节点的下一个节点
    const ret = cur.next;
    // 断开循环链表
    cur.next = null;
    // 返回新的头节点
    return ret;
};

分隔链表（中）

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当保留两个分区中每个节点的初始相对位置。

示例 1：

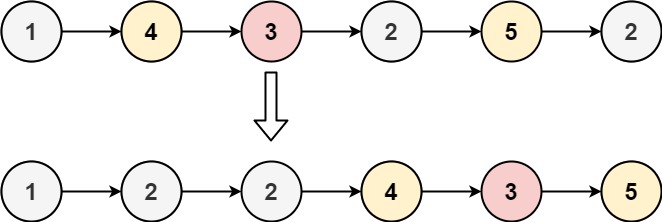
输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

示例 2：

输入：head = [2,1], x = 2
输出：[1,2]

提示：

链表中节点的数目在范围 [0, 200] 内
-100 <= Node.val <= 100
-200 <= x <= 200

解题思路

初始化两个新链表：创建两个新链表，一个用于存储所有值小于x的节点（称为小链表），另一个用于存储所有值大于或等于x的节点（称为大链表）。
遍历原始链表：遍历原始链表的每个节点。
根据值的大小进行分类：对于当前遍历的节点，如果其值小于x，则将该节点添加到小链表的末尾；如果其值大于或等于x，则将该节点添加到大链表的末尾。
连接两个链表：遍历完成后，将小链表的末尾连接到大链表的头节点，从而形成一个新链表。
返回新链表的头节点：返回新链表的头节点，即小链表的下一个节点（因为小链表的头节点是初始化时创建的空节点）。

这个函数的核心思想是通过两个辅助链表来组织原始链表的节点，从而在不改变节点原始顺序的前提下，根据节点的值将它们分成两部分。

var partition = function (head, x) {
    // 创建两个新节点，分别作为小于x的节点链和大于等于x的节点链的头节点
    let small = new ListNode();
    const smallHead = small;
    let large = new ListNode();
    const largeHead = large;

    // 遍历原始链表
    while (head) {
        // 如果当前节点的值小于x
        if (head.val < x) {
            // 将当前节点添加到小于x的链表中
            small.next = head;
            small = small.next;
        } else {
            // 否则，将当前节点添加到大于等于x的链表中
            large.next = head;
            large = large.next;
        }
        // 移动到链表的下一个节点
        head = head.next;
    }

    // 确保大于等于x的链表的末尾是null
    large.next = null;
    // 将小于x的链表的末尾连接到大于等于x的链表的头节点
    small.next = largeHead.next;
    // 返回新的链表头节点，即小于x的链表的头节点的下一个节点
    return smallHead.next;
};

二叉树的右视图（中）

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:

输入: [1,null,3]
输出: [1,3]

示例 3:

输入: []
输出: []

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

解题思路

首先递归地遍历右子树，然后遍历左子树。这样，我们总是先到达每层的最右侧节点。当深度等于结果数组的长度时，我们添加当前节点值，这样就只记录了每层最右侧的节点值。

var rightSideView = function (root) {
    const result = []
    function dfs(node, depth) {
        if (node === null) return;
        if(depth === result.length) {
            result.push(node.val)
        }
        dfs(node.right, depth + 1);
        dfs(node.left, depth + 1);
    }
    dfs(root, 0);
    return result
};

昵称

邮箱

网址

按正序
按倒序
按热度

案例

反转链表(简)

环形链表(简)

两数相加(中)

合并两个有序链表(简)

随机链表的复制(中)

反转链表 II(中)

K 个一组翻转链表（难）

删除链表的倒数第 N 个结点（中）

删除排序链表中的重复元素 II（中）

旋转链表（中）

分隔链表（中）

二叉树的右视图（中）

预览: